Pipelining

5.1. Overview of Pipelining

Efficient computation by discovering that we can overlay single-cycle datapaths in time to produce a type of computational architecture called pipelining. We show that pipelined architectures, when they work properly and are relatively free from errors and hazards such as dependencies, stalls, or exceptions can outperform a simple multicycle datapath. Also, we discuss problems associated with pipelining that limits its usefulness in various types of computations.

5.1.1. Concept of Pipelining

Suppose you wanted to make an automobile from scratch. You might gather up the raw materials, form the metal into recognizeable shapes, cast some of the metal into an engine block, connect up fuel lines, wires, etc., to eventually (one would hope) make a workable automobile. To do this, you would need many skills - all the skills of the artisans that make autos, and management skills in addition to being an electrician and a metallurgist. This would not be an efficient way to make a car, but would definitely provide many challenges.

That is the way a multicycle datapath works - it is designed to do everything - input, output, and computation (recall the fetch-decode-execute sequence). We need to ask ourselves if this is really the best way to compute efficiently, especially when we consider the complexity of control for large (CISC) systems or even smaller RISC processors.

Fortunately, our analogy with car-making is not so far-fetched, and can actually help us arrive at a more efficient processor design. Consider the modern way of making cars - on an assembly line. Here, there is an orderly flow of parts down a conveyor belt, and the parts are processed by different stations (also called segments of the assembly line). Each segment does one thing, over and over. The segments are coordinated to exploit the sequentiality inherent in the automobile assembly process. The work gets done more smoothly (because of the orderly flow of input parts and output results), more efficiently (because each assembler at each segment of the pipeline does his or her task at what one hopes is maximum efficiency), and more reliably because there is greater consistency in one task being done repetitively (provided the assembly line is designed correctly).

A similar analogy exists for computers. Instead of a multicycle datapath with its complex control system that walks, talks, cries, and computes - let us suppose that we could build an assembly line for computing. Such objects actually exist, and they are called pipeline processors. They have sequentially-arranged stages or segments, each of which perform a specific task in a fixed amount of time. Data flows through these pipelines like cars through an assembly line.

5.1.2. Definitions and Practical Observations about Pipelines

We next consider several terms and some practical issues associated with pipeline processors.

5.1.2.1. Definition. A pipeline processor is comprised of a sequential, linear list of segments, where each segment performs one computational task or group of tasks.

5.1.2.2. Observation. A pipeline processor can be represented in two dimensions, as shown in Figure 5.1. Here, the pipeline segments (Seg #1 through Seg #3) are arranged vertically, so the data can flow from the input at the top left downward to the output of the pipeline (after Segment 3). The progress of an instruction is charted in blue typeface, and the next instruction is shown in red typeface.

There are three things that one must observe about the pipeline. First, the work (in a computer, the ISA) is divided up into pieces that more or less fit into the segments alloted for them. Second, this implies that in order for the pipeline to work efficiently and smoothly, the work partitions must each take about the same time to complete. Otherwise, the longest partition requiring time T would hold up the pipeline, and every segment would have to take time T to complete its work. For fast segments, this would mean much idle time. Third, in order for the pipeline to work smoothly, there must be few (if any) exceptions or hazards that cause errors or delays within the pipeline. Otherwise, the instruction will have to be reloaded and the pipeline restarted with the same instruction that causes the exception. There are additional problems we need to discuss about pipeline processors, which we will consider shortly.

Figure 5.1. Notional diagram of a pipeline processor. The segments are arranged vertically, and time moves along the horizontal axis.

5.1.2.3. Reponse Time. It is easily verified, through inspection of Figure 5.1., that the response time for any instruction that takes three segments must be three times the response time for any segment, provided that the pipeline was full when the instruction was loaded into the pipeline. As we shall see later in this section, if an N-segment pipeline is empty before an instruction starts, then N + (N-1) cycles or segments of the pipeline are required to execute the instruction, because it takes N cycles to fill the pipe.

Note that we just used the term "cycle" and "segment" synonomously. In the type of pipelines that we will study in this course (which includes the vast majority of pipeline processors), each segment takes one cycle to complete its work. Thus, an N-segment pipeline takes a minimum time of N cycles to execute one instruction. This brings to mind the performance issues discussed in Section 5.1.1.5.

5.1.2.4. Work Partitioning. In the previous section, we designed a multicycle datapath based on the assumption that computational work associated with the execution of an instruction could be partitioned into a five-step process, as follows:

5.1.2.5. Performance. Because there are N segments active in the pipeline at any one time (when it is full), it is thus possible to execute N segments concurrently in any cycle of the pipeline. In contrast, a purely sequential implementation of the fetch-decode-execute cycle would require N cycles for the longest instruction. Thus, it can be said that we have O(N) speedup. As we shall see when we analyze pipeline performance, an exact N-fold speedup does not always occur in practice. However it is sufficient to say that the speedup is of order N.

5.2. Pipeline Datapath Design and Implementation

As shown in Section 5.1.2.4, the work involved in an instruction can be partitioned into steps labelled IF (Instruction Fetch), ID (Instruction Decode and data fetch), EX (ALU operations or R-format execution), MEM (Memory operations), and WB (Write-Back to register file). We next discuss how this sequence of steps can be implemented in terms of MIPS instructions.

5.2.1. MIPS Instructions and Pipelining

In order to implement MIPS instructions effectively on a pipeline processor, we must ensure that the instructions are the same length (simplicity favors regularity) for easy IF and ID, similar to the multicycle datapath. We also need to have few but consistent instruction formats, to avoid deciphering variable formats during IF and ID, which would prohibitively increase pipeline segment complexity for those tasks. Thus, the register indices should be in the same place in each instruction. In practice, this means that the rd, rs, and rt fields of the MIPS instruction must not change location across all MIPS pipeline instructions.

Additionally, we want to have instruction decoding and reading of the register contents occur at the same time, which is supported by the datapath architecture that we have designed thus far. Observe that we have memory address computation in the lw and sw instructions only, and that these are the only instructions in our five-instruction MIPS subset that perform memory operations. As before, we assume that operands are aligned in memory, for straightforward access.

5.2.2. Datapath Partitioning for Pipelining

Recall the single-cycle datapath, which can be partitioned (subdivided) into functional units as shown in Figure 5.2. Because the single-cycle datapath contains separate Instruction Memory and Data Memory units, this allows us to directly implement in hardware the IF-ID-EX-MEM-WB representation of the MIPS instruction sequence. Observe that several control lines have been added, for example, to route data from the ALU output (or memory output) to the register file for writing. Also, there are again three ALUs, one for ALUop, another for JTA computation, and a third for adding PC+4 to compute the address of the next instruction.

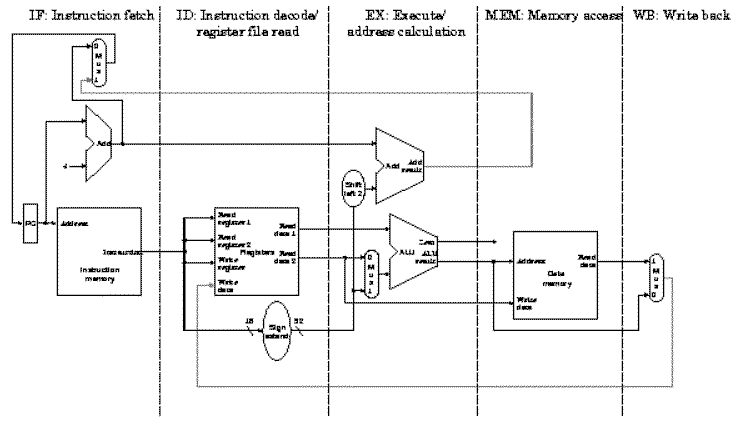
Figure 5.2. Partitioning of the MIPS single-cycle datapath developed previously, to form a pipeline processor. The segments are arranged horizontally, and data flows from left to right [Maf01,MK98].

We can represent this pipeline structure using a space-time diagram similar to Figure 5.1, as shown in Figure 5.3. Here four load instructions are executed sequentially, which are chosen because the lw instruction is the only one in our MIPS subset that consistently utilizes all five pipeline segments. Observe also that the right half of the register file is shaded to represent a read operation, while the left half is shaded to represent write.

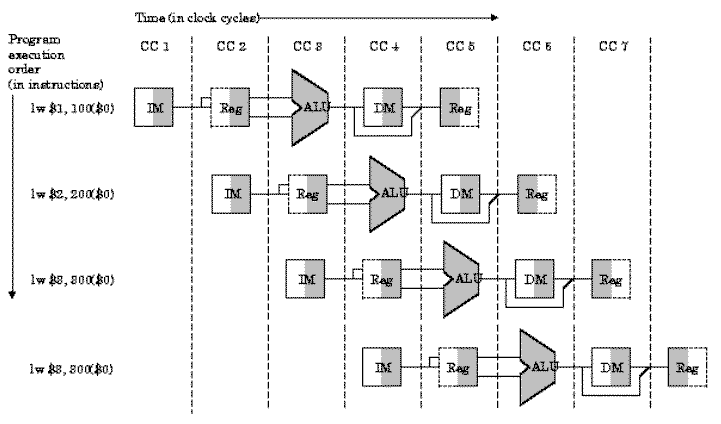
Figure 5.3. Partitioning of the MIPS single-cycle datapath developed previously, with replication in space, to form a pipeline processor that computes four lw instructions. The segments are arranged horizontally, and data flows from left to right, synchronously with the clock cycles (CC1 through CC7) [Maf01,MK98].

In order to ensure that the single-cycle datapath conforms to the pipeline design constraint of one cycle per segment, we need to add buffers and control between stages, similar to the way we added buffers in the multicycle datapath. These buffers and control circuitry are shown in Figure 5.4 as red rectangles, and store the results of the i-th stage so that the (i+1)-th stage can use these results in the next clock cycle.

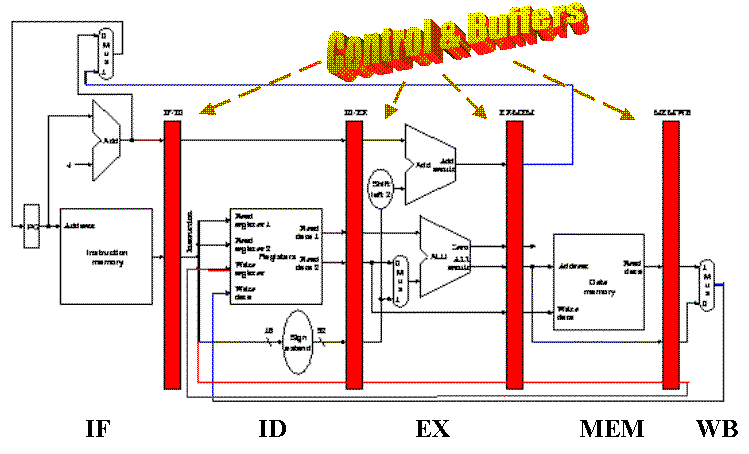
Figure 5.4. Addition of control and buffer circuits to Figure 5.3 produces the MIPS pipelined datapath [Maf01,MK98].

In summary, pipelining improves efficiency by first regularizing the instruction format, for simplicity. We then divide the instructions into a fixed number of steps, and implement each step as a pipeline segment. During the pipeline design phase, we ensure that each segment takes about the same amount of time to execute as other segments in the pipeline. Also, we want to keep the pipeline full wherever possible, in order to maximize utilization and throughput, while minimizing set-up time.

In the next section, we will see that pipeline processing has some difficult problems, which are called hazards, and the pipeline is also susceptible to exceptions.

5.3. Pipeline Control and Hazards

Reading Assignments and Exercises

The control of pipeline processors has similar issues to the control of multicycle datapaths. Pipelining leaves the meaning of the nine control lines unchanged, that is, those lines which controlled the multicycle datapath. In pipelining, we set control lines (to defined values) in each stage for each instruction. This is done in hardware by extending pipeline registers to include control information and circuitry.

5.3.1. Pipeline Control Issues and Hardware

Observe that there is nothing to control during instruction fetch and decode (IF and ID). Thus, we can begin our control activities (initialization of control signals) during ID, since control will only be exerted during EX, MEM, and WB stages of the pipeline. Recalling that the various stages of control and buffer circuitry between the pipeline stages are labelled IF/ID, ID/EX, EX/MEM, and MEM/WB, we have the propagation of control shown in Figure 5.5.

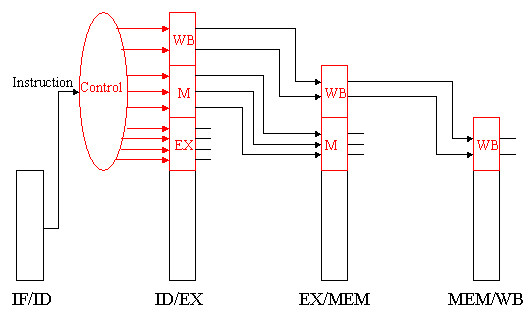
Figure 5.5. Propagation of control through the EX, MEM, and WB states of the MIPS pipelined datapath [Maf01,MK98].

Here, the following stages perform work as specified:

• IF/ID: Initializes control by passing the rs, rd, and rt fields of the instruction, together with the opcode and funct fields, to the control circuitry.
• ID/EX: Buffers control for the EX, MEM, and WB stages, while executing control for the EX stage. Control decides what operands will be input to the ALU, what ALU operation will be performed, and whether or not a branch is to be taken based on the ALU Zero output.
• EX/MEM: Buffers control for the MEM and WB stages, while executing control for the MEM stage. The control lines are set for memory read or write, as well as for data selection for memory write. This stage of control also contains the branch control logic.
• MEM/WB: Buffers and executes control for the WB stage, and selects the value to be written into the register file.

Figure 5.6 shows how the control lines (red) are arranged on a per-stage basis, and how the stage-specific control signals are buffered and passed along to the next applicable stage.

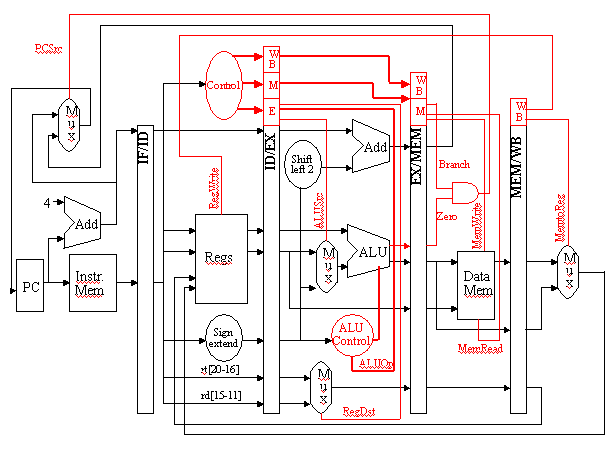
Figure 5.6. Propagation of control through the EX, MEM, and WB states of the MIPS pipelined datapath [Maf01,MK98].

5.3.2. Overview of Hazards

Pipeline processors have several problems associated with controlling smooth, efficient execution of instructions on the pipeline. These problems are generally called hazards, and include the following three types:

• Structural Hazards occur when different instructions collide while trying to access the same piece of hardware in the same segment of a pipeline. This type of hazard can be alleviated by having redundant hardware for the segments wherein the collision occurs. Occasionally, it is possible to insert stalls or reorder instructions to omit this type of hazard.
• Data Hazards occur when an instruction depends on the result of a previous instruction still in the pipeline, which result has not yet been computed. The simplest remedy inserts stalls in the execution sequence, which reduces the pipeline's efficiency. The solution to data dependencies is twofold. First, one can forward the ALU result to the writeback or data fetch stages. Second, in selected instances, it is possible to restructure the code to eliminate some data dependencies. Forwarding paths are shown as thin blue or red lines in Figure 5.4.
• Control Hazards can result from branch instructions. Here, the branch target address might not be ready in time for the branch to be taken, which results in stalls (dead segments) in the pipeline that have to be inserted as local wait events, until processing can resume after the branch target is executed. Control hazards can be mitigated through accurate branch prediction (which is difficult), and by delayed branch strategies.

We next examine hazards in detail, and discuss several techniques for eliminating or relieving hazards.

5.3.3. Data Hazards

Definition. A data hazard occurs when the current instruction requires the result of a preceding instruction, but there are insufficient segments in the pipeline to compute the result and write it back to the register file in time for the current instruction to read that result from the register file.

We typically remedy this problem in one of three ways:

• Forwarding: In order to resolve a dependency, one adds special circuitry to the pipeline that is comprised of wires and switches with which one forwards or transmits the desired value to the pipeline segment that needs that value for computation. Although this adds hardware and control circuitry, the method works because it takes far less time for the required value(s) to travel through a wire than it does for a pipeline segment to compute its result.
• Code Re-Ordering: Here, the compiler reorders statements in the source code, or the assembler reorders object code, to place one or more statements between the current instruction and the instruction in which the required operand was computed as a result. This requires an "intelligent" compiler or assembler, which must have detailed information about the structure and timing of the pipeline on which the data hazard would occur. We call this type of software a hardware-dependent compiler.
• Stall Insertion: It is possible to insert one or more stalls (no-op instructions) into the pipeline, which delays the execution of the current instruction until the required operand is written to the register file. This decreases pipeline efficiency and throughput, which is contrary to the goals of pipeline processor design. Stalls are an expedient method of last resort that can be used when compiler action or forwarding fails or might not be supported in hardware or software design.
  The following example is illustrative.

  Example. Suppose we have the following sequence of instructions:

       sub   $2,   $1,   $3   # Register 2 is the output of sub
       and   $8,   $2,   $5   # Operand #1 depends on Register 2 data
       or    $9,   $6,   $2   # Operand #2 depends on Register 2 data
       add   $7,   $2,   $2   # Add result depends on Register 2 data
       sw    $6,20($2)        # Store (memory write) depends on Register 2
  

  whose pipeline scheduling diagram is shown in Figure 5.7.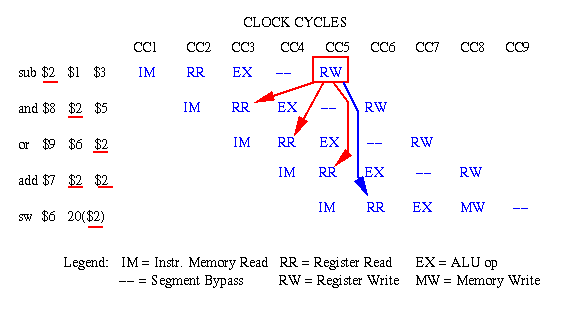

  
  
  Figure 5.7. Example of data hazards in a sequence of MIPS instructions, where the red (blue) arrows indicate dependencies that are problematic (not problematic) [Pat98,MK98].

  Problem: The first instruction (sub), starting on clock cycle 1 (CC1) completes on CC5, when the result in Register 2 is written to the register file. If we did nothing to resolve data dependencies, then no instruction that read Register 2 from the register file could read the "new" value computed by the sub instruction until CC5. The dependencies in the other instructions are illustrated by solid lines with arrowheads. If register read and write cannot occur within the same clock cycle (we will see how this could happen in Section 5.3.4), then only the fifth instruction (sw) can access the contents of register 2 in the manner indicated by the flow of sequential execution in the MIPS code fragment shown previously.

  Solution #1 - Forwarding: The result generated by the sub instruction can be forwarded to the other stages of the pipeline using special control circuitry (data bus switchable to any other segment, which can be implemented via a decoder or crossbar switch). This is indicated notionally in Figure 5.7 by solid red lines with arrowheads. If the register file can read in the first half of a cycle and write in the second half of a cycle, then the forwarding in CC5 is not problematic. Otherwise, we would have to delay the execution of the add instruction by one clock cycle (see Figure 5.9 for insertion of a stall).

  Solution #2 - Code Re-Ordering: Since all Instructions 2 through 5 in the MIPS code fragment require Register 2 as an operand, we do not have instructions in that particular code fragment to put between Instruction 1 and Instruction 2. However, let us assume that we have other instructions that (a) do not depend on the results of Instructions 1-5, and (b) themselves induce no dependencies in Instructions 1-5 (e.g., by writing to register 1, 2, 3, 5, or 6). In that case, we could insert two instructions between Instructions 1 and 2, if register read and write could occur concurrently. Otherwise, we would have to insert three such instructions. The latter case is illustrated in the following figure, where the inserted instructions and their pipeline actions are colored dark green.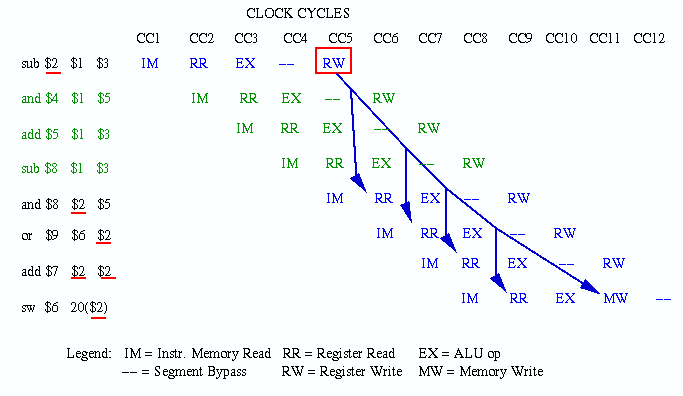

  
  
  Figure 5.8. Example of code reordering to solve data hazards in a sequence of MIPS instructions [Pat98,MK98].

  Solution #3 - Stalls: Suppose that we had no instructions to insert between Instructions 1 and 2. For example, there might be data dependencies arising from the inserted instructions that would themselves have to be repaired. Alternatively, the program execution order (functional dependencies) might not permit the reordering of code. In such cases, we have to insert stalls, also called bubbles, which are no-op instructions that merely delay the pipeline execution until the dependencies are no longer problematic with respect to pipeline timing. This is illustrated in Figure 5.9 by inserting three stalls between Instructions 1 and 2.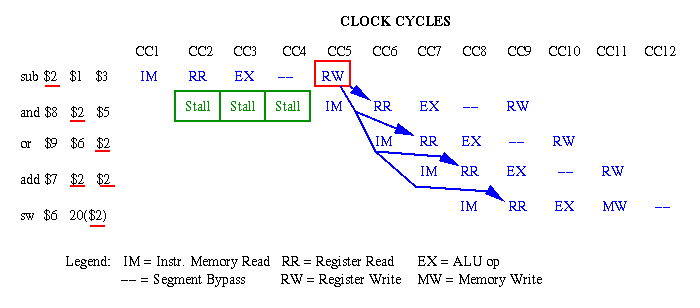

  
  
  Figure 5.9. Example of stall insertion to solve data hazards in a sequence of MIPS instructions [Pat98,MK98].

  As mentioned previously, the insertion of stalls is the least desireable technique because it delays the execution of an instruction without accomplishing any useful work (in contrast to code re-ordering).

  5.3.4. Structural Hazards

  Definition. A structural hazard occurs when there is insufficient hardware to support a computation in a given pipeline segment.
  For example, consider the data dependency between the first and fourth instructions (sub and add) of the example in Section 5.3.3. Here, a register file write and a register file read are scheduled in CC5. This can be resolved by (a) duplicating hardware, or (b) modifying the existing hardware to support concurrent operations. If we duplicated the register file, then we could perform concurrent read and write operations, but there would be a consistency problem. That is, at a given clock cycle, registers in one register file could have different values than the corresponding registers in the other register file. This inconsistency is clearly unacceptable if accurate computation is to be maintained.
  Instead, we can modify the register file so that it (1) performs register write on the first half of the clock cycle and (2) performs register read on the second half of the clock cycle. In earlier hardware, designers sometimes inserted a delay between write and read that was very small in relation to the clock cycle time, in order to ensure convergence of the register file write.
  Other structural hazards could occur during the branch instruction, if there were not two ALUs in the EX segment of the pipeline. That is, with only one ALU, we would have to simultaneously compute the BTA and determine (via subtraction) whether or not the branch condition was fulfilled. This would not be possible without two concurrent adders in the ALU, which is what we currently have in our MIPS pipeline design shown in Figure 5.4.
  A further structural hazard could occur if we only used one memory for both instructions and data. For example, in Figure 5.7, suppose the sub instruction was instead a sw instruction. Then, we would be writing to data memory in CC4 for Instruction #1 and reading from instruction memory in CC4 for Instruction #4. Clearly, if there was only one memory there would be a conflict.
  Similar to the problem with the concurrent reads and writes on the register file, there are two ways to solve this dilemma. First, we can design a special-purpose memory module that permits writing (reading) on the first (resp. second) half of the clock cycle, as we said could be done with the register file. However, this requires special (expensive) hardware. Second, we can use two fast caches, one for instructions, and one for data, that access a large, slower main memory in which instructions and data are both stored. The latter method is used in practice because caches and main memory already exist, and the memory management hardware for these types of components also exists. Thus, we can use off-the-shelf hardware to solve a problem that would otherwise require special-purpose development of expensive hardware. Although this might not be as much fun as developing new hardware, it is more cost-effective, which matters when one is designing and producing computers for profit.

  5.3.5. Control (Branch) Hazards

  Control hazards are the most difficult types of hazards arising from normal operation of a program. In the next section, we will see that exceptions (e.g., overflow) can play particularly interesting types of havoc with smooth pipeline execution.
  The most common type of control hazard is the branch instruction, which has two alternative results: (1) jump to the branch target address if the instruction succeeds, or (2) execute the instruction after the branch (at PC+4 of instruction memory) if the branch fails.
  The problem with the branch instruction is that we usually do not know which result will occur (i.e., whether or not the branch will be taken) until the branch condition is computed. Often, the branch condition depends on the result of the preceding instruction, so we cannot precompute the branch condition to find out whether or not the branch will be taken.
  The following four strategies are employed in resolving control dependencies due to branch instructions.
  5.3.5.1. Assume Branch Not Taken. As we saw previously, we can insert stalls until we find out whether or not the branch is taken. However, this slows pipeline execution unacceptably. A common alternative to stalling is to continue execution of the instruction stream as though the branch was not taken. The intervening instructions between the branch and its target are then executed. If the branch is not taken, this is not a harmful or disruptive technique. However, if the branch is taken, then we must discard the results of the instructions executed after the branch statement. This is done by flushing the IF, ID, and EX stages of the pipeline for the discarded instructions. Execution continues uninterrupted after the branch target.
  The cost of this technique is approximately equal to the cost of discarding instructions. For example, if branches are not taken 50 percent of the time, and the cost of discarding results is negligible, then this technique reduces by 50 percent the cost of control hazards.
  5.3.5.2. Reducing Branch Delay. In the MIPS pipeline architecture shown schematically in Figure 5.4, we currently assume that the branch condition is evaluated in Stage 3 of the pipeline (EX). If we move the branch evaluation up one stage, and put special circuitry in the ID (Decode, Stage #2), then we can evaluate the branch condition for the beq instruction. This would allow us to take the branch in EX instead of MEM, since we would have ready for Stage 3 (EX) the Zero output of the comparator that would normally be computed in EX. The hardware needed to compute equality is merely a series of parallel xnor gates and-ed together, then inverted.

  Exercise: Determine how this type of circuitry could be configured.

  The advantage of this technique is that only one instruction needs to be discarded rather than two, as in the previous section. This reduces hardware cost and time required to flush the pipeline, since only the IF and ID stages would need to be flushed, instead of the three stages in the preceding example.
  5.3.5.3. Dynamic Branch Prediction. It would be useful to be able to predict whether or not a majority of the branches are taken or not taken. This can be done in software, using intelligent compilers, and can also be done at runtime. We concentrate on the software-intensive techniques first, since they are less expensive to implement (being closer to the compiler, which is easier to modify than the hardware).
  The most advantageous situation is one where the branch condition does not depend on instructions immemdiately preceding it, as shown in the following code fragment:

       add $5, $5, $6     # One of the registers for beq comparison is modified
       sub $4, $3, $6     # Nothing important to the branch here
       and $7, $8, $6     # Nothing important to the branch here
       and $9, $6, $6     # Nothing important to the branch here
       beq $5, $6, target
  

  Here, the branch compares Registers 5 and 6, which are last modified in the add instruction. We can therefore precompute the branch condition as sub r $5, $6, where r denotes a destination register. If r = 0, then we know the branch will be taken, and the runtime module (pipeline loader) can schedule the jump to the branch target address with full confidence that the branch will be taken.
  Another approach is to keep a history of branch statements, and to record what addresses these statements branch. Since the vast majority of branches are used as tests of loop indices, then we know that the branch will almost always jump to the loopback point. If the branch fails, then we know the loop is finished, and this happens only once per loop. Since most loops are designed to have many iterations, branch failure occurs less frequently in loops than does taking the branch.
  Thus, it makes good sense to assume that a branch will jump to the place that it jumped to before. However, in dense decision structures (e.g., nested or cascaded if statements), this situation does not always occur. In such cases, one might not be able to tell from the preceding branch whether or not the branching behavior will be repeated. It is then reasonable to use a multi-branch lookahead.

  Reading Assigment: Study the discussion of multi-bit branch prediction schemes given on pp. 501-502 of the textbook.

  Another clever technique of making branches more efficient is the branch delay slot. We previously discussed delayed branches when we overviewed the multicycle datapath implementation of the beq instruction. In summary, the concept of efficient branching has two parts. First, the branch target address is computed in the ID stage of the pipeline, to determine as early as possible the instruction to fetch if the branch succeeds. Since this is done in the second stage of the pipeline, there is an instruction I following this (in the first or IF stage). After I moves to the ID stage, then the branch target (pointed to by either PC+4 or the BTA) is loaded into the IF stage.
  It is this instruction (I) that is called the branch delay slot (BDS). In the BDS can be safely placed an instruction that does not have data dependencies with respect to (a) the branch condition, (b) the instruction following the branch condition, or (c) the branch target. This ensures that, when the instruction J is executed (J is the instruction to which control is transferred after the branch condition is evaluated, whether J is pointed to by PC+4 or BTA), then the instruction I will have been executed previously, and the pipe will not have a stall where I would have been. As a result, the pipe will remain full throughout the branch evaluation and execution, unless an exception occurs.

  5.3.6. Exceptions as Hazards

  Hardware and software must work together in any architecture, especially in a pipeline processor. Here, the ISA and processor control must be designed so that the following steps occur when an exception is detected:
  1. Hardware detects an exception (e.g., overflow in the ALU) and stops the offending instruction at the EX stage.
  2. Pipeline loader and scheduler allow all prior instructions (e.g., those already in the pipeline in MEM and WB) to complete.
  3. All instructions that are present in the pipeline after the exception is detected are flushed from the pipeline.
  4. The address of the offending instruction (usually the address in main memory) is saved in the EPC register, and a code describing the exception is saved in the Cause register.
  5. Hardware control branches to the exception handling routine (part of the operating system).
  6. The exception handler performs one of three actions: (1) notify the user of the exception (e.g., divide-by-zero or arithmetic-overflow) then terminate the program; (2) try to correct or mitigate the exception then restart the offending instruction; or (3) if the exception is a benign interrupt (e.g., an I/O request), then save the program/pipeline state, service the interrupt request, then restart the program at the instruction pointed to by EPC + 4.
  In any case, the pipeline is flushed as described.
  In general, we can say that, if a pipeline has N segments, and the EX stage is at segment 1 < i < N, then two observations are key to the prediction of pipeline performance:
  • Flushing negates the processing of the (i-1) instructions following the offending instruction. These must be reloaded into the pipe, at the cost of i cycles (one cycle to flush, i-1 cycles to reload the i-1 instructions after the exception is processed).
  • Completing the N-i instructions that were loaded into the pipeline prior to the offending instruction takes N-i clock cycles, which are executed (a) prior to, or (b) concurrently with, the reloading of the instructions i-1 that followed the i-th instruction (in the EX stage).
  It is readily seen that the total number of wasted cycles equals (i-1) + (N-i) = N - 1, which is precisely the number of cycles that it takes to set up or reload the pipeline.
  The proliferation of unproductive cycles can be mitigated by the following technique:
  1. Freeze the pipeline state as soon as an exception is detected.
  2. Process the exception via the exception handler, and decide whether or not to halt or restart the pipeline.
  3. If the pipeline is restarted, reload the (i-1) instructions following the offending instruction, concurrently with completing execution of the (N-i) instructions that were being processed prior to the offending instruction.
  If Step 3 can be performed as stated, then the best-case penalty is only one cycle, plus the time incurred by executing the exception handler. If the entire pipeline needs to be flushed and restarted, then the worst-case penalty is N cycles incurred by flushing the pipe, then reloading the pipeline after the instructions preceding the offending instruction have been executed. If the offending instruction must be restarted, then a maximum of i cycles are lost (one cycle for flush, plus (i-1) cycles to restart the instructions in the pipe following the offending instruction).
  In the next section, we collect the concepts about pipeline performance that we have been discussing, and show how to compute the CPI for a pipeline processor under constraint of stalls, structural hazards, branch penalties, and exception penalties.

  5.4. Pipeline Performance Analysis

  Reading Assignments and Exercises
  
  As we said early on in this course, we are trying to teach the technique of performance analysis, which helps one to intelligently determine whether or not a given processor is suitable computationally for a specific application. In this section, we develop performance equations for a pipeline processor, and do so in a stepwise way, so you can see how the various hazards and penalties affect performance.

  5.4.1. CPI of a Pipeline Processor

  Suppose an N-segment pipeline processes M instructions without stalls or penalties. We know that it takes N-1 cycles to load (setup) the pipeline, and M cycles to complete the instructions. Thus, the number of cycles is given by:
  N_cyc = N + M - 1 .
  The cycles per instruction are easily computed:
  CPI = N_cyc/M = 1 + (N - 1)/M .
  Thus, CPI for a finite program will always be greater than one. This stands in sharp contradiction to the first fallacy of pipeline processing, which says:

  Fallacy #1: CPI of a pipeline processor is always equal to 1.0, since one instruction is processed per cycle.

  This statement is fallacious because it ignores the overhead that we have just discussed. The fallacy is similar to claiming that you only spend eight hours at the office each day, so you must have 16 hours per day of "fun time". However, you have to take time to commute to/from the office, buy groceries, and do all the other homely tasks of life, many of which are in no way related to "fun time". In practice, such tasks are drudgery that is a type of overhead.

  5.4.2. Effect of Stalls

  Now let us add some stalls to the pipeline processing scheme. Suppose that we have a N-segment pipeline processing M instructions, and we must insert K stalls to resolve data dependencies. This means that the pipeline now has a setup penalty of N-1 cycles, as before, a stall penalty of K cycles, and a processing cost (as before) of M cycles to process the M instructions. Thus, our governing equations become:
  N_cyc = N + M + K - 1 .
  and
  CPI = N_cyc/M = 1 + (N + K - 1)/M .
  In practice, what does this tell us? Namely, that the stall penalty (and all the other penalties that we will examine) adversely impact CPI. Here is an example to show how we would analyze the problem of stalls in a pipelined program where the percentage of instructions that incur stalls versus non-stalls are specified.

  Example. Suppose that an N-segment pipeline executes M instructions, and that a fraction f_stall of the instructions require the insertion of K stalls per instruction to resolve data dependencies. The total number of stalls is given by f_stall · M · K (fraction of instructions that are stalls, times the total number of instructions, times the average number of stalls per instruction). By substitution, our preceding equations for pipeline performance become:

  N_cyc = N + M + (f_stall · M · K) - 1 .

  and

  CPI = N_cyc/M = 1 + (f_stall · K) + (N - 1)/M .

  So, the CPI penalty due to the combined effects of setup cost and stalls now increases to fK + (N - 1)/M. If f_stall = 0.1, K = 3, N = 5, and M = 100, then CPI = 1 + 0.3 + 4/100 = 1.34, which is 34 percent larger than the fallacious assumption of CPI = 1.

  This leads to the next fallacy of pipeline processing:

  Fallacy #2: Stalls are not a big problem with pipelines - you only have to worry about the number of stalls, not the percentage of instructions that induce stalls.

  This fallacy is particularly dangerous. It is analogous to saying that the only thing that matters is the number of home burglaries each year, not the burglary rate per capita. If you move to a new neighborhood, you want to know both the number and per-capita incidence of crimes in that neighborhood, not just the robbery count. Then you can determine, from the population, whether or not it is safe to live there.
  Similarly, with a pipeline processor, you want to determine whether or not the instruction mix or ordering of instructions causes data dependencies, and what is the incidence of such dependencies. For example, 1,000 instruction program with 20 stalls will run more efficiently than a 1,000 instruction program with 20 percent of the instructions requiring one stall each to resolve dependencies.

  5.4.3. Effect of Exceptions

  For purposes of discussion, assume that we have M instructions executing on an N-segment pipeline with no stalls, but that a fraction f_ex of the instructions raise an exception in the EX stage. Further assume that each exception requires that (a) the pipeline segments before the EX stage be flushed, (b) that the exception be handled, requiring an average of H cycles per exception, then that (c) the instruction causing the exception and its following instructions be reloaded into the pipeline.
  Thus, f_ex · M instructions will cause exceptions. In the MIPS pipeline, each of these instructions causes three instructions to be flushed out of the pipe (IF, ID, and EX stages), which incurs a penalty of four cycles (one cycle to flush, and three to reload) plus H cycles to handle the exception. Thus, the pipeline performance equations become:
  N_cyc = N - 1 + (1 - f_ex) · M + (f_ex · M · (H + 4)) ,
  which we can rewrite as
  N_cyc = M + [N - 1 - M + (1 - f_ex) · M + (f_ex · M · (H + 4))] .
  Rearranging terms, the equation for CPI can be expressed as
  CPI = N_cyc/M = 1 + [1 - f_ex + (f_ex · (H+4)) - 1 + (N - 1)/M] .
  After combining terms, this becomes:
  CPI = N_cyc/M = 1 + [(f_ex · (H+3)) + (N - 1)/M] .
  We can see by examination of this equation and the expression for CPI due to stalls that exceptions have a more detrimental effect, for two reasons. First, the overhead for stalls (K stalls per affected instruction) is K < 4 cycles in the MIPS pipeline (since the pipeline has only five segments). Second, the cost of each exception is H+3 cycles per affected instruction. Since H > 0 for a nontrivial exception handler, the cost of an exception in the MIPS pipeline (under the preceding assumptions) will exceed the cost of remedying a hazard using stalls. The good news, however, is that there are usually fewer exceptions in programs than data or structural dependencies, with the exception of I/O-intensive programs (many I/O interrupts) and arithmetic-intensive programs (possible overflow or underflow exceptions).

  5.4.4. Effect of Branches

  Branches present a more complex picture in pipeline performance analysis. Recall that there are three ways of dealing with a branch: (1) Assume the branch is not taken, and if the branch is taken, flush the instructions in the pipe after the branch, then insert the instruction pointed to by the BTA; (2) the converse of 1); and (3) use a delayed branch with a branch delay slot and re-ordering of code (assuming that this can be done).
  The first two cases are symmetric. Assume that an error in branch prediction (i.e., taking the branch when you expected not to, and conversely) requires L instruction to be flushed from the pipeline (one cycle for flushing plus L-1 "dead" cycles, since the branch target can be inserted in the IF stage). Thus, the cost of each branch prediction error is L cycles. Further assume that a fraction f_br of the instructions are branches and f_be of these instructions result in branch prediction errors.
  The penalty in cycles for branch prediction errors is thus given by
  branch_penalty = f_br · f_be · M instructions · L cycles per instruction .
  The pipeline performance equations then become:
  N_cyc = N - 1 + (1 - f_br · f_be) · M + (f_br · f_be · M · L) ,
  which we can rewrite as
  N_cyc = M + [N - 1 - M + (1 - f_br · f_be) · M + (f_br · f_be · M · L) ,
  Rearranging terms, the equation for CPI can be expressed as
  CPI = N_cyc/M = 1 + [(1 - f_br · f_be) + (f_br · f_be · L) - 1 + (N - 1)/M] .
  After combining terms, this becomes:
  CPI = N_cyc/M = 1 + [(f_br · f_be · (L-1)) + (N - 1)/M] .
  In the case of the branch delay slot, we assume that the branch target address is computed and the branch condition is evaluated at the ID stage. Thus, if the branch prediction is correct, there is no penalty. Depending on the method by which the pipeline evaluates the branch and fetches (or pre-fetches) the branch target, a maximum of two cycles penalty (one cycle for flushing, one cycle for fetching and inserting the branch target) is incurred for insertion of a stall in the case of a branch prediction error. In this case, the pipeline performance equations become:
  N_cyc = N - 1 + (1 - f_br · f_be) · M + (f_br · f_be · 2M) ,
  which implies the following equation for CPI as a function of branches and branch prediction errors:
  CPI = N_cyc/M = 1 + [f_br · f_be + (N - 1)/M] .
  Since f_br << 1 is usual, and f_be is, on average, assumed to be no worse than 0.5, the product f_br · f_be, which represents the additional branch penalty for CPI in the presence of delayed branch and BDS, is generally small.