Clipping

Clipping

Since we have a separation between the models and the image created from those models, there can be parts of the model that do not appear in the current view when they are rendered.
pixels outside the clip rectangle are clipped, and are not displayed.
can clip analytically - knowing where the clip rectangle is clipping can be done before scan-line converting a graphics primitive (point, line, polygon) by altering the graphics primitive so the new version lies entirely within the clip rectangle
can clip by brute force (scissoring) - scan convert the entire primitive but only display those pixels within the clip rectangle by checking each pixel to see if it is visible.

• clipping a point against a rectangle -> nothing or single point
• clipping a line against a rectangle -> nothing or single line segment
• clipping a rectangle against a rectangle -> nothing or single rectangle
  • ( Assuming the rectangle is aligned. Otherwise treat as convex polygon. )
• clipping a convex polygon against a rectangle -> nothing or single single convex polygon
• clipping a concave polygon against a rectangle -> nothing or 1 or more concave polygons

as with scan conversion, this must be done as quickly as possible as it is a very common operation.

---

Point Clipping

point (X,Y)
clipping rectangle with corners (Xmin,Ymin) (Xmax,Ymax)
point is within the clip rectangle if:

Xmin <= X<= Xmax
Ymin <= Y<= Ymax

---

Cohen-Sutherland Line Clipping ( Foley 3.12.3 )

given a line segment, repeatedly:

1. check for trivial acceptance
   both endpoints within clip rectangle
2. check for trivial rejection
   both endpoints outside clip rectangle IS NOT ENOUGH
   both endpoints off the same side of clip rectangle IS ENOUGH
3. divide segment in two where one part can be trivially rejected

Clip rectangle extended into a plane divided into 9 regions
each region is defined by a unique 4-bit string

• left bit = 1: above top edge (Y > Ymax)
  • left bit = sign bit of (Ymax - Y)
• 2nd bit = 1: below bottom edge (Y < Ymin)
  • 2nd bit = sign bit of (Y - Ymin)
• 3rd bit = 1: right of right edge (X > Xmax)
  • 3rd bit = sign bit of (Xmax - X)
• right bit = 1: left of left edge (X < Xmin)
  • right bit = sign bit of (X - Xmin)

(the sign bit being the most significant bit in the binary representation of the value. This bit is '1' if the number is negative, and '0' if the number is positive.)
The frame buffer itself, in the center, has code 0000.

1001 | 1000 | 1010
-----+------+-----
0001 | 0000 | 0010
-----+------+-----
0101 | 0100 | 0110

For each line segment:

1. each end point is given the 4-bit code of its region
2. repeat until acceptance or rejection
   1. if both codes are 0000 -> trivial acceptance
   2. if bitwise logical AND of codes is not 0000 -> trivial rejection
   3. divide line into 2 segments using edge of clip rectangle
      1. find an endpoint with code not equal to 0000
      2. move left to right across the code to find a 1 bit -> the crossed edge
      3. break the line segment into 2 line segments at the crossed edge
      4. forget about the new line segment lying completely outside the clip rectangle

The full algorithm ( was? ) given (in C) in the red book ( ??? Edition ) as program 3.7 on p.105.
The full algorithm is given (in C) in the white book as figure 3.41 on p.116.

Sutherland-Hodgman Polygon Clipping ( Foley 3.14.1 )

Unlike line-clipping where we selectively clipped against each edge, here we sucessively clip a polygon against all four edges of the clip rectangle
given a polygon with vertices V1, V2, ... Vn
and edges between vertices Vi and Vi+1, and from Vn to V1
for each of the four clipping edges

repeatedly for each vertex V = Vn, V1, V2, ... Vn


given an edge from vertex s to vertex p
assume s has already been dealt with


• if s and p are both inside the clip rectangle -> output p
• if s is inside and p is outside the clip rectangle -> output i (the intersection of edge sp with the clip edge)
• if s and p are both outside the clip rectangle -> output nothing
• if s is outside and p is inside the clip rectangle -> output i (the intersection of edge sp with the clip edge) and then p
output edges become new set of polygon edges

This algorithm can break a single polygon into multiple polygons connected by edges on the boundary of the clipping rectangle for display.
The full algorithm ( was? ) given (in C) in the red book ( ??? Ediiton ) as program 3.9 on p.114.
The full algorithm is given (in Pascal) in the white book as program 3.49 on p.128.

---

Example of Polygon Clipping

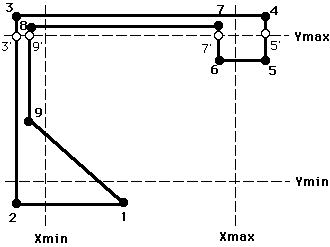
Clipping on Ymax edge:

• 9-1 : both inside -> add 1
• 1-2 : both inside -> add 2
• 2-3 : keep 2-3' and clip 3'-3 -> add 3'
• 3-4 : both outside -> add nothing
• 4-5 : keep 5'-5 and clip 4-5' -> add 5' and 5
• 5-6 : both inside -> add 6
• 6-7 : keep 6-7' and clip 7'-7 -> add 7'
• 7-8 : both outside -> add nothing
• 8-9 : keep 9'-9 and clip 8-9' -> add 9' and 9
• 9-1 : both inside -> add 1
• returning 1,2,3',5',5,6,7',9',9 as the new vertex sequence

the new vertex sequence is then checked against the Ymin edge and so on through the Xmax edge and the Xmin edge

---

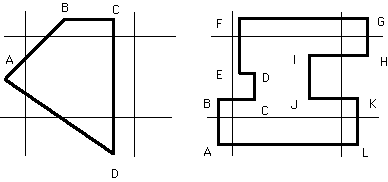
2 More Examples