Overview of Computer Abstractions
As shown in Figure 1.1, computer systems span many
levels of detail, which in computer science we call levels of
abstraction. This hierarchy is reviewed in Appendix
B.
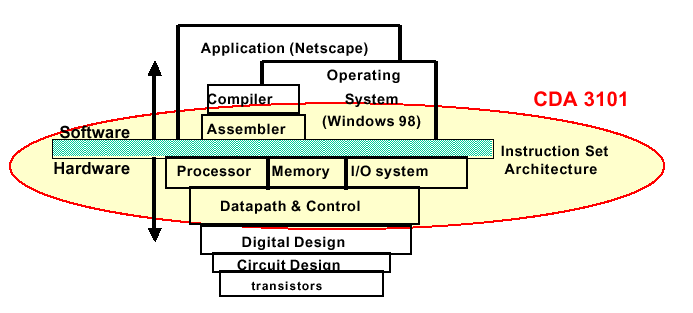
Figure 1.1. Levels of abstraction in computer systems, adapted from [Maf01]
In this course, we are concerned with the
following components:
- Operating System - Provides a convenient interface between (a) the user and his/her application software, and (b) the hardware (sometimes called the bare machine).
- Assembler - Translates assembly language, a primitive type of programming language, into machine code, which is a stream of ones and zeroes.
- Instruction Set Architecture(ISA) - Interfaces the software (listed above) to the hardware (listed below), and provides support for programming.
- Processor, Memory, and I/O System - These components support the execution of machine code instructions expressed in terms of the ISA.
- Datapath and Control - Provide a convenient abstraction for connecting the processor, memory, and I/O system and controlling their function efficiently.
If you have taken Dr. Mafla's version of this
course, you will be acquainted with the following five components
of a computer:
- Input - Provides data and program information
- Datapath - Mediates I/O
- Control - Implements control of calculation and communication or I/O processes
- Memory - Storage and retrieval of programs or data
- Output - Result of running program on processor using input
1.2. Overview of Computer Abstractions
Abstractions help us express intangible concepts in
visible representations that can be manipulated. For example, a
data structure is an abstraction that organizes concepts or numbers
in a comprehensible, organized representation that can be manipulated
by a computer program. Figure 1.2 illustrates another view of a
computer system, which is comprised of different levels of language
and means of translating these languages into lower-level languages. Finally,
the microprogram is loaded onto the hardware.
1.2.1. Different Abstract Views
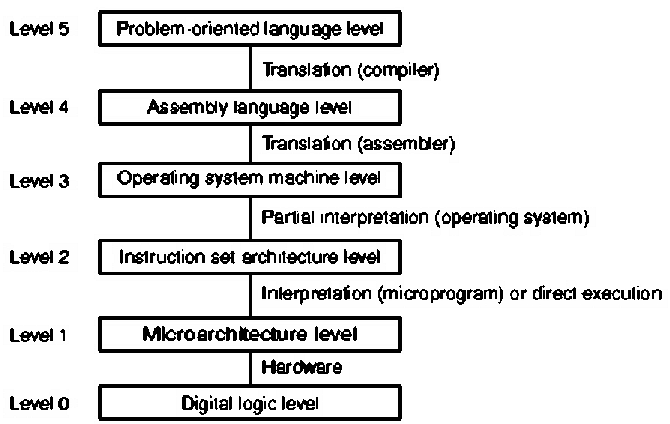
Figure 1.2. Another view of levels of abstraction in computer systems, adapted from [Maf01].
The salient concepts for Figure 1.2 are listed as follows:
- Level 5 - Problem Oriented Language - Provides a convenient interface and applications engine that helps the user produce results specific to a given application area. For example, Microsoft Word is used for document creation or editing, Excel for accounting spreadsheets, etc. The language at this level is usually a sequence of keystrokes or a high-level scripting language. In software design, the language is a high-level programming language such as C, C++, or Java.
- Level 4 - Assembly Language - Assembly is a very detailed language that helps the systems programmer or software designer move information around in a computer architecture in a highly specific way. For example, many compilers (programs that translate programming language into an assembly-like language) are written in assembly language. The advantage to assembly language is speed and power in accessing various features of the hardware.
- Level 3 - Operating System Machine - Provides a convenient interface between assembly language and the abstraction of the hardware architecture's instruction set. Operating systems generally contain many libraries that help a software developer or programmer connect to lower-level system functions (e.g., I/O, memory allocation, etc.) in an organized way.
- Level 2 - Instruction Set Architecture (ISA) - One of the most important parts of a computer is the interface between the lowest-level software and the hardware. The ISA includes anything programmers use to make a binary machine language program work correctly, including instructions, I/O, etc. The ISA facilitates design of functionality independent of the hardware.
- Level 1 - Microarchitectural Level - Microinstructions are low-level control instructions that define the set of datapath control signals which apply to a given state of a computing machine. The microinstructions, together with their sequencing, comprise the microarchitecture, whose purpose is to rigorously and consistently express the control of logic circuits that comprise the computer hardware. Designing this control in terms of a program that implements machine instructions in terms of simpler microinstructions is called microprogramming.
- Level 0 - Digital Logic - The circuitry that makes a digital computer run is called logic. All processes of a digital computer are expressed in terms of functions of ones and zeros, for example, and, or, and not functions. We will review these logic functions in Section 1.4.
A more general view of the abstractions shown in
Figure 1.2 is given in Figure 1.3. Note the recursive levels of
translation, from an actual machine (digital logic level in Figure 1.2)
to various virtual machines (higher levels of abstraction).
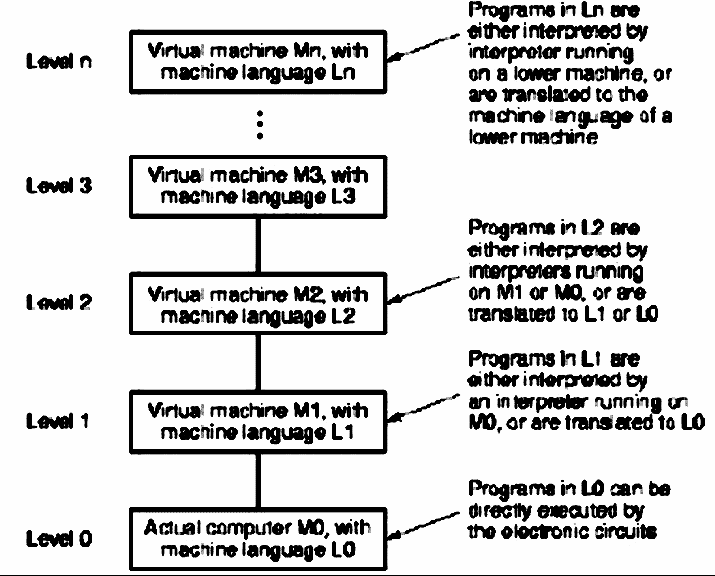
Figure 1.3. Generalized view of levels of abstraction in computer systems, adapted from [Maf01].
This leads to the following implementational view,
where the scope of this course is circled in red.
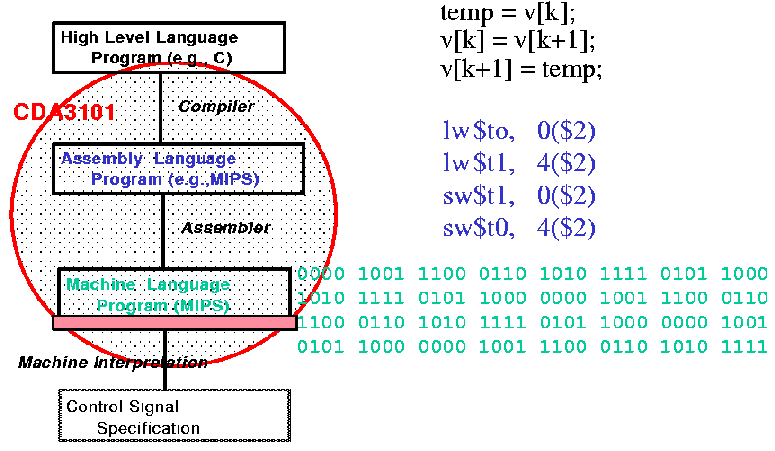
Figure 1.4. Another view of levels of abstraction in computer systems, adapted from [Maf01].
1.2.2. RISC versus CISC
When computers were first developed, they had very
small instruction sets, because the algorithms and hardware for
complicated tasks had not yet been developed. As computer design
continued into the 1960s, high-level languages (e.g., FORTRAN, Cobol,
Lisp) evolved. Hardware designers formed the idea that it might be
useful to develop different computers for each type of language -
a FORTRAN machine, a COBOL machine, etc. When this approach was tried,
it resulted in very complicated instruction sets. Parallel to this
development was the IBM philosophy of upward compatibility, which they
also tried to implement in hardware. This produced a huge collection
of instructions to support all their old computer programs (called
legacy code). The result of this was called Complex Instruction
Set Computing (CISC), whose philosophy is summarized as follows:
- Bigger is better!
- Make the hardware as "smart" (and, hence, as complex) as possible.
- If you have a great sprawling architecture, that's ok. The hardware fabricators will figure out what to do with your design.
- Don't worry about whether or not the system design is neatly partitioned into layers. (One great sea of logic gates would be ok until we figure out something else that works.)
- When one little part fails, the whole system dies and we will never find out why. That's ok - just build another CPU chip from the ground up. Maybe that one will work better.
CISC has many problems. Some of the bigger problems
include lack of maintainability, lack of verifiability,
and brittleness. In practice, humans don't know how to verify
or maintain really complicated designs. And, we don't yet have
software that can perform all the verification and maintenance tasks
for us. As a result, as CISC machines got more and more complex, they
failed considerably more frequently. This yielded brittle
(non-robust) performance in practical computing problems. As the
world became more dependent on computers, the CISC design philosophy
gradually became unacceptable.
In response to this problem, computer designers
returned back to the primitive roots of computer science, and
developed the Reduced Instruction Set Computing (RISC) philosophy.
The main concept in RISC is that of a very simple Instruction Set
Architecture. There is a compact microinstruction set, into which
every high-level command or instruction is translated by the compiler.
RISC computers tend to run faster, are smaller, and have fewer
problems because they have a simple instruction set. The RISC
philosophy includes the following concepts:
- Small is beautiful.
- Keep the hardware simple and stupid (KISS design philosophy).
- Hardware and software designers should work together to make the architecture simple and modular.
- Neatly partition the system design into layers, as shown in Figures 1.2 and 1.3. Then, take the vast majority of the functionality that CISC implements in hardware, and put it into software (using compiler transformations) instead.
- Make the hardware and compiler robust, so the entire system can perform reliably.
By keeping the hardware small and modular, the design
and fabrication, maintenance, and debugging costs are reduced. This
makes sense from an economic perspective. It is also easier to make
new generations of RISC computer chips, and to produce them more
quickly. This implies potentially greater profits by shortening both
the development and product life cycles.
Modularity and simplicity in hardware and software
help designers and engineers achieve greater robustness, because the
system can be maintained and understood more easily. With simple
hardware and software, the functionality of the design can be verified
more extensively using software-based testing and
proof-of-correctness. Finally, it makes sense to put the CISC
complexity into the compiler software, because the software can be
modified and corrected much more easily, inexpensively, and quickly
than hardware can be changed or updated. Again, this makes good
economic sense, because development and re-work costs are
significantly reduced.
1.2.3. Concept Summary
Thus far, we have seen that computer hardware
(software) evolved in the following stepwise fashion:
- Step 1. - Bare logic circuits (plugboard based programming)
- Step 2. - Microarchitectural control (machine language programming)
- Step 3. - Operating system (batch -> multiprogramming -> time-sharing -> parallelism)
- Step 4. - Complex architectures (compilers for high-level languages, e.g., FORTRAN, COBOL -> Pascal -> C -> C++ -> Java)
- Step 5. - Hardware/Software interface development (ISA -> CISC -> RISC)
1.3. Overview of Computer Technology Trends
In Section 1.1, we briefly summarized how technology
developed from vacuum tube circuits to modern VLSI techniques. The
ability to place more logic gates per unit area has been the primary
motivation for exponentially increasing memory and processor capacity
and performance. This development has followed several important
trends, which we discuss in this section, as follows.
1.3.1. Memory Capacity
Memory capacity has approximately doubled every 1.5
years since the early 1970s. Prior to that, memory was not
implemented in integrated circuits, but consisted of arrays of tiny
magnetic cores strung together on a lattice of fine wires. Thus, the
origin of the term core to describe a computer's main memory.
Figure 1.5 illustrates the memory capacity trend, showing how memory
gate density has increased from 1 mbegabit (Mbit) per chip in 1986 to 256
Mbit per chip in 2000. By 2004, this is expected to reach 1 Gbit per
chip.
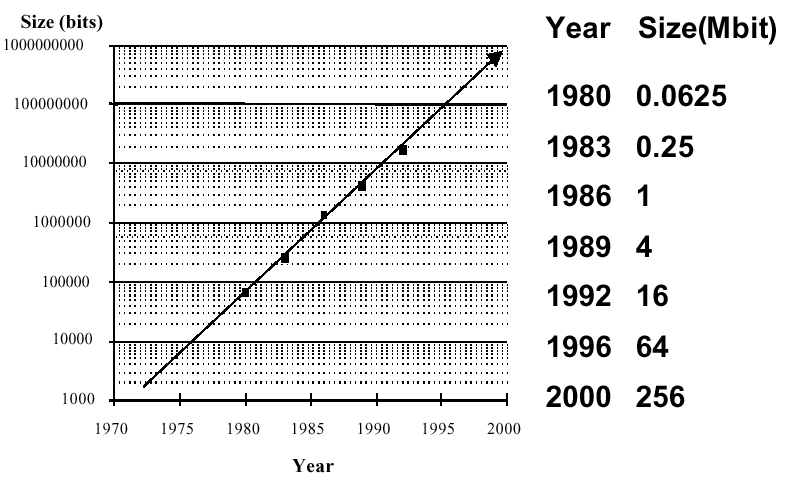
Figure 1.5. Exponential increase in memory capacity as a function of time since the early 1970s, adapted from [Maf01].
The increase in memory capacity and processor
performance (Section 1.3.3) has made it possible to migrate
supercomputer applications such as sophisticated image enhancement,
finite-element modelling, and weather prediction to desktop computers.
However, this rate of increase is probably not sustainable on
an indefinite basis, as discussed in Section 1.3.4.
1.3.2. Processor Capacity
The number of transistors per chip has approximately
doubled every 1.5 years since the early 1970s, when integrated
circuits became available. This effect is called Moore's Law.
Figure 1.6 illustrates this trend, showing how chip size has increased
from fewer than 2,000 transistors in 1970 to over 15 million
transistors in 2000. By 2003, this is expected to reach 60 million
transistors per chip.
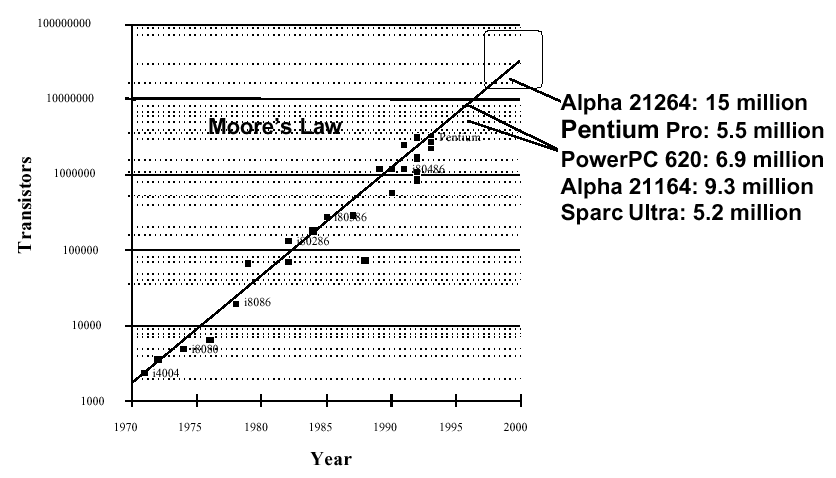
Figure 1.6. Exponential increase in processor capacity as a function of time since the early 1970s (Moore's Law), adapted from [Maf01].
The increase in processor capacity has made it
possible to increase the speed of processor circuitry, particularly
for arithmetic logic operations. For example, the chip area (also
called real estate) required by an N-digit multiplier circuit
varies approximately as N2. Thus, if the processor area
doubles every 1.5 years, then the speed increase of a multiplier
possible with such technology could increase by a factor of
21/2 = 1.414 times every 1.5 years. We see this reflected
in the performance increases shown in the following section.
1.3.3. Processor Performance
In order to measure processor performance, we use the
units of SPEC benchmarks. The System Performance Evaluation
Cooperative (SPEC) benchmark suite was created in 1989 to rpovide a
consistent set of realistic benchmarks for evaluating CPU performance.
The SPEC95 set of benchmarks includes games, a hardware simulator,
file compression and decompression, applications such as quantum
physics simulations, fluid dynamics problem solutions, and so forth.
In Figure 1.7, we show the increase in processor performance as a
function of the SPEC92 benchmark suite, which is listed in Gee et al.'s
analysis of cache performance. (Cache is a type of fast
memory that we will discuss later in this course.)
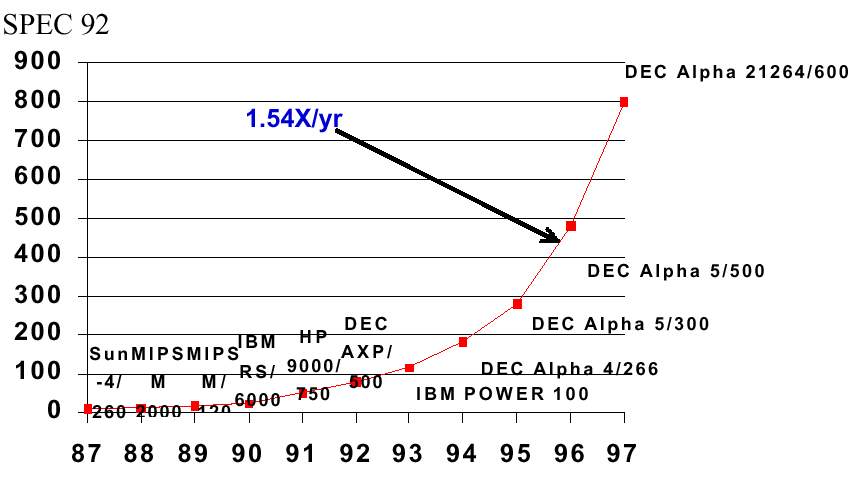
Figure 1.7. Exponential increase in processor performance as a function of time since the early 1970s, adapted from [Maf01].
The increase in processor performance has made it
possible to port real-world applications to the PC platforms (e.g.,
Pentium and Apple G4 PC architectures). In the preceding section, we
said that a multiplier's speed could increase 1.414 times every 1.5
years. So why does the curve in Figure 1.7 show an increase in
processor capacity of 1.54 times per year? Consider that, although
the previously-mentioned N-digit multiplier requires area proportional
to N2, there exist many operations that only need area
proportional to N. The mix of these applications and the operations
that they use is highly dependent on the applications being run on the
computer. Hence, the use of a benchmark suite such as SPEC92 or
SPEC95 (discussed in the textbook), to provide a consistent mix
of operations across all platforms and test scenarios.
1.3.4. Physical Limits on Computer Capacity and Performance
In the preceding presentation of hardware technology
trends, there is danger in assuming that these trends will continue
forever. In fact, there are physical limits to computer chip size and
speed, which we will discuss briefly in this section.
Currently, computer chips are made by a process
called lithography, in which the chip design is laid out with
the aid of a computer, then printed onto a master template having
multiple layers. This template is called a lithograph, after
the printing process of that name. Masks are made from the lithograph
master and are used to allow (or mask) the penetration of high-energy
radiation into the semiconductor materials that comprise the chip.
This irradiation process supports chemical removal of materials that
comprise the partially completed semiconductor circuit, which is called
etching.
Present lithography processes support 0.18 micron
resolution (size of the smallest feature that can be produced on the
chip). Making these dimensions smaller, to pack more transistors on
the chip, requires the lithography process to use wavelengths of
electromagnetic energy that are much smaller than visible light.
Thus, it is foreseen that litho processes will progress through the
ultraviolet range, down into X-ray and gamma-ray lithography, as
technology is developed.
However, the limiting constraint is not how small we
can make features on a circuit board. Rather, the hard limit involved
in using computer circuits that we have today is dictated by the size
of an atom. For example, when the thickness of an insulating strip
between two conductors on a circuit board becomes less than
approximately 1.2 atomic diameters, then there is significant
interference or cross-talk between conductors or
channels in an information-carrying structure called a
bus. Given today's resolution of 0.18 microns, and the limiting
atomic dimension of approximately 1nm (0.001), we only have approximately
a factor of 200, or less than 2.5 orders of magnitude increase in
resolution left in the current technology. That translates to a capacity
increase of approximately 2502 = 62,500, which is not a
comforting margin of safety. If Moore's Law continues to hold, then
we the number of capacity-doubling periods is given by
Np = log2(62,500) < 16 ,
which translates to less than 16(1.5) = 24 years left
in the technology cycle. Dr. Moore's current estimate is that we will
run out of capacity in 2017, others say as late as 2025. What is
certain is, that within your professional lifetime as computer
scientists, there will be a radical shift from current circuit
technology to something different - a technology that will support
much faster, more highly parallel computing. Perhaps quantum
computing will emerge as the dominant technology. Others say that
biological
computers based on DNA or protein technology will come to the
rescue. IBM has recently announced the possibility of building
circuits from carbon
nanotubes, which presently have a width of approximately 10 atomic
diameters. Whatever will happen, the paradigm shift will have
profound technological and economic effects on the computer industry.
There is an interesting article about future
technology trends at CNN's Web site that discusses Extreme
Ultraviolet Photolithography for chip making - a useful summary of
things that might occur.
If you want to read more about physical limits on
computing, visit Dr. Frank's Web page
about physical limits on computation. He has taught a course
in this area, and the references listed therein make for interesting
reading.
We next present overview of the types of computer
architectures that have been developed with the technologies that have
evolved since the dawn of useable computers during WWII.
1.3.5. Types of Architectures
There are three principal ways to connect components
in a computer, called the von Neumann, bus, and
multiprocessor architectures. We summarize each of these, as
follows.
1.3.5.1. von Neumann Architecture. John von
Neumann elucidated the first practical stored-program computer
architecture (scheme for connecting computer components) in the
mid-1940s. It is comprised of the five classical components (input,
output, processor, memory, and datapath). The processor is divided
into an arithmetic logic unit (ALU) and control unit, a method of
organization that persists to the present. Within the processor, the
ALU datapath mediates data transfer for computation. The
registers are fast memory modules from/to which data can be
read/written to support streaming computation, as shown in Figure 1.8.
Within the ALU, an accumulator supports efficient addition or
incrementation of values corresponding to variables such as loop
indices.
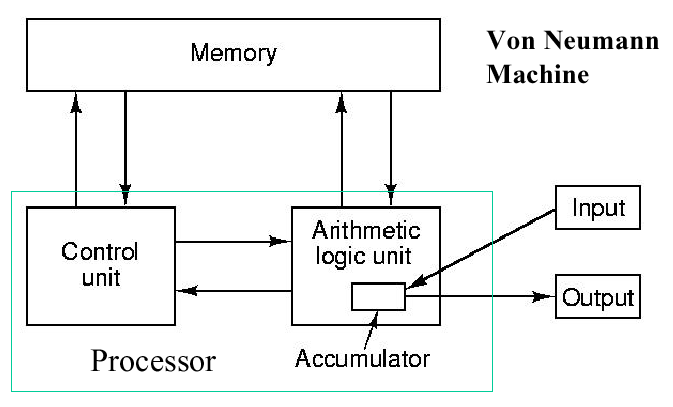
Figure 1.8. Schematic diagram of von Neumann architecture, adapted from [Maf01].
The von Neumann architecture has a significant
disadvantage - its speed is dependent on the bandiwdht or throughput
of the datapath between the processor and memory. This is called the
von Neumann bottleneck.
1.3.5.2. Bus Architecture. There are many
animals (e.g., cat or dog) whose internal organs are hung from a
backbone that conveniently happens to be horizontal. Bus-based
computers are structured like that - processors and memory are
connected to a backbone bus that acts as a "superhighway" for
data or instructions to move between processors and memory. In
practice, the bus architecture has the same components as the von
Neumann architecture, but they are arranged along a bus, as shown
in Figure 1.9.
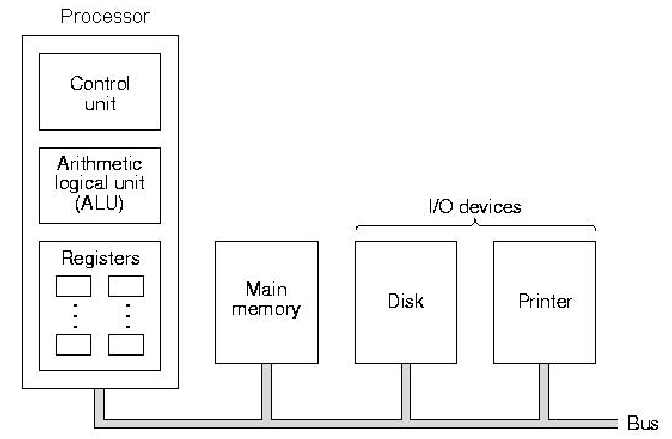
Figure 1.9. Schematic diagram of a bus architecture, adapted from [Maf01].
In principle, the bus computer solves the von Neumann
bottleneck problem by using a fast bus. In practice, the bus is
rarely fast enough to support I/O for the common case (90 percent of
practical applications), and bus throughput can be significantly reduced
under large amounts of data. Figure 1.10 shows the
layout of components in a modern PC, which is a useful example of a bus
architecture.
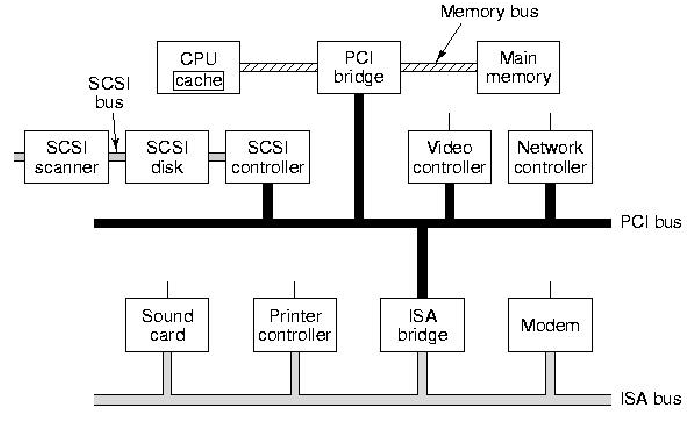
Figure 1.10. Schematic diagram of PC bus architecture, adapted from [Maf01].
In Figure 1.10, note that there are multiple buses -
the PCI bus mediates large-scale data transfer between external
components, as does the ISA bus. The SCSI bus is used to daisy chain
peripherals such as disk drives, scanner, etc. The von Neumann
bottleneck is partially overcome in practice by using a very fast bus,
called the memory bus, to connect the CPU, memory, and the PCI
bus.
Unfortunately, there are physical limits on how many
components can be packed in a given space in a von Neumann machine
(or any other computer, for that matter). Bus bandwidth limits the
sequential computation model inherent in the von Neumann architecture
to speeds that are not feasible for compute-intensive scientific
applications. As a result, multiprocessor architectures were developed
to address such problems, as discussed in the following section.
1.3.5.3. Multiprocessor or Parallel
Architecture. Recall the old saying, "Many hands make less work."
In computers, the use of many processors together reduces the amount
of time required to perform the work of solving a given problem. Due
to I/O and routing overhead, this efficiency is sublinear in the
number of processors. That is, if W(N) [or T(N)] denotes the work [or
time to perform the work] associated with N processors, then the
following relationships hold in practice:
W(N) < N · W(1)
and
T(N) > T(1)/N .
The first equation means that the work performed by N
processors working on a task, where each processor performs work W(1)
[the work of one processor in a sequential computation paradigm], will
be slightly less than N times W(1). Note that we use "<" instead of
"=" because of the overhead required to (1) divide up the problem, (2)
assign the parts of the problem to N processors, (3) collect the
partial results from the N processors, and (4) combine the partial
results to achieve a whole, coherent result.
The second equation means essentially the same thing
as the first equation, but the work is replaced by time. Here, we are
saying that if one processor takes time T(1) to solve a problem, then
that same problem solved on an N-processor architecture will take time
slightly greater than T(1)/N, assuming all the processors work together at the
same time. As in the preceding paragraph, this discrepancy is due to
the previously-described overhead.
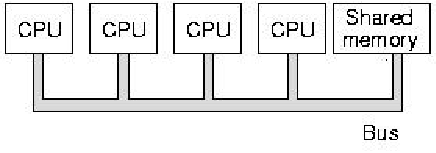
Figure 1.11. Schematic diagram of multiprocessor architecture, where each CPU shares a memory module that is connected to a common bus - adapted from [Maf01].
Figure 1.11 illustrates schematically a simple
multiprocessor architecture with four CPUs, which share a memory
module that is connected to the CPUs via a common bus. This is a
simple architecture that is useful for solving selected types of
compute-intensive problems. However, if you try to solve
data-intensive problems on such an architecture, you encounter the von
Neumann bottleneck trying to read and write the large amount of data
from and to the shared memory.
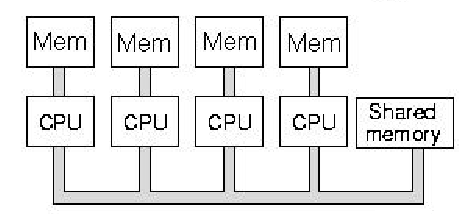
Figure 1.12. Schematic diagram of multiprocessor architecture with shared memory, where each CPU also has its own fast, local memory - adapted from [Maf01].
To help solve the problem of bus contention
inherent in shared-memory multiprocessors, computer scientists
developed the mixed model of parallel processing, in which the CPUs
have small, very fast local memories that communicate with the CPU via
a very fast, short bus. Because the bus is short, there are fewer
impedance problems and the bus bandwidth can be increased. This
migrates the von Neumann bottleneck closer to the CPU, and alleviates
some of the demands on shared memory. Local memory architectures are
useful for problems that have data locality, where (1) each CPU
can solve part of a problem with part of the problem's data, and (2)
there is little need for data interchange between processors.
A special type of multiprocessor is called a
distributed processor, in which the individual CPUs (called
compute servers) are connected to storage servers by a network.
You can make the multiprocessor diagrammed schematically in Figure 1.12
into a distributed computer by replacing with a network the bus that
connects the CPUs to each other and to the shared memory.
Having taken a high-level tour through computer technology
trends, we next examine the low-level technology that makes these machines
work, namely, digital logic.
1.4. Digital Logic Design
Digital logic is hardware that implements the
functions of Boolean algebra, which are or, and, not,
as well as combinations of these functions. Boolean algebra
operations are extensively employed in computing, and form the
basis for the vast majority of arithmetic operations, as we shall
see later in this course.
We begin this section by discussing the operands
and operations that comprise Boolean algebra, then show how these
logical operations are implemented in simple digital devices.
1.4.1. Theory of Logical Operations
The kind of logic that we use in computing is
generally called formal logic, which is one of the three bases
of mathematics. (The other two bases are measurement theory and
algebraic manipulation.) The type of formal logic that we will use in
this course is called Boolean logic or Boolean algebra
(the terms are interchangeable). There are other types of formal
logics, such as interval logic (often called fuzzy logic), but
we will not consider them in this course.
Definition. An algebra is a tuple
A = (F,O) that contains a set of values
F and a set of operations O on those values.
Example. The algebra of real numbers
contains operations such as addition, multiplication, and
division, with operands selected from the real numbers R.
Definition. Boolean algebra
B = ({0,1}, O) contains a set of operations O called
logical-or, logical-and, logical-not, etc.,
that operate upon numbers in the set {0,1} (i.e., operate on
zero(es) or one(s)).
Example: logical-not - The not
function inverts the value of its input. Thus, 0 = not(1) and
1 = not(0). Because the not function has only one
input, it is called a unary operation.
Example: logical-and - The and
function takes the minimum of its two inputs. Thus,
0 = and(0,0) = and(0,1) = and(1,0). However, 1 =
and(1,1). Because the and function has two inputs, it
is called a binary operation. (This use of the word "binary" is
similar to calling the set {0,1} the "binary numbers", because there
are only two numbers in the set.)
Example: logical-or - The or
function takes the maximum of its two inputs. Thus,
0 = or(0,0), with 1 = or(0,1) = or(1,0) =
or(1,1).
It is important to note that all logical operations
can be constructed from not and and. In your discrete
mathematics course (COT3100 at UF/CISE), you will see (or have seen)
how to do this. For now, it is useful to accept this assertion and
continue on.
We next consider how digital logic is represented in
term of truth tables and graphic symbols used in circuit diagrams. In
Section 1.4.3, we will discuss how digital logic can be implemented in
hardware.
1.4.2. Representations of Digital Logic
When we are working with digital logic, it is easy
to describe the functionality of a logic device in terms of a truth
table.
Definition. A truth table is a tabular
representation of a logical operation that completely defines the
operation.
Observation. A logical operation with N inputs
will have 2N entries in its truth table. If an operation
has many inputs, then its truth table can be represented compactly by
listing only those entries that have nonzero output.
There are also a variety of graphic symbols that are
used with digital logic functions. In Figure 1.13, we show the
symbols for the and as well as or gates, with their
truth table representations. If we represented these truth tables
compactly, then the and operation would have only one row in
its truth table, namely, [1 1 1].
Self-Exercise. How many rows are there in the compact representation of the or operation's truth table, and what are these rows?
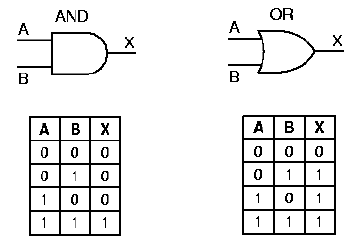
Figure 1.13. Graphic symbols and truth tables for the logic gates that implement and as well as or operations, adapted from [Maf01].
The not gate is represented graphically as
shown in Figure 1.14a. By appending a circle to the output of a gate
symbol, we can represent the effect of putting a not gate after
the gate represented by the symbol. For example, the output of the
and gate is inverted by the not gate to form the nand
gate, as shown in Figure 1.14b. A similar situation is shown for the
nor gate in Figure 1.14c. Note that the truth table for the
nand operation has three nonzero entries, whereas the truth
table for the and operation had only one nonzero entry. A
symmetric condition exists for the nor operation.
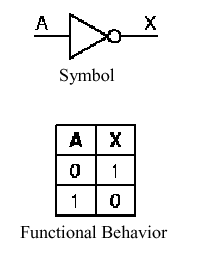
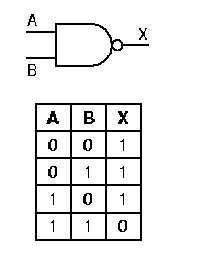
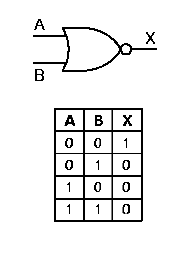
Figure 1.14. Graphic symbols and truth tables for negative logic gates that implement (a) not, (b) nand, (c) nor operations - adapted from [Maf01].
In the next section, we discuss how these basic
gates are implemented in electronic circuits.
1.4.3. Circuit Implementation of Digital Logic
In 1947, scientists at Bell Laboratories developed
the transistor, which is a circuit element whose conductivity
varies with applied voltage. The advantage of the transistor is that
a relatively small input current can be used to control a much larger
power-supply current. The general concept involved in the operation
of the transistor is similar to that of the vacuum tube (recall our
discussion of first-generation computers), but requires much
less power and space. Also, the transistor can change state much more
quickly than a vacuum tube - as sometimes said in electrical
engineering, the transistor has a higher switching frequency.
1.4.3.1. Simple Model of A Transistor NOT
Gate. Figure 1.15 shows a diagram of a transistor that implements
negative logic. Note that the collector supply voltage
Vcc is positive, and the current from this power source
flows through a current limiting resistor, whose symbol is the jagged
line below Vcc. The resistor is designed to prevent
damage to the transistor junction, which is delicate. (This
junction is comprised of several semiconducting materials deposited on
a small wafer of silicon or germanium called substrate. As we
discussed in Section 1.3, the dimensions of features etched into the
substrate are presently on the order of 0.2 micron, so it doesn't take
much excess current to cause electrical arcing across these features,
which renders the transistor useless.)
A control voltage (shown in Figure 1.15 as the
input signal A) is applied to the base of the transistor. If A
= 0, the conductivity of the transistor is low, and the current from
the collector is not grounded at the emitter. This causes a voltage
difference to be present between the emitter (at ground) and the
collector (at Vcc). Symmetrically, when A = 1 (i.e., a
voltage significantly higher than zero), then the conductivity of the
transistor is enhanced, and Vcc is grounded. This produces
little or no voltage drop across the collector-emitter junction, and
the output at the collector is effectively zero. When the output of
the transistor is taken from the collector (as shown in Figure 1.15),
these two conditions cause a not operation to be implemented.
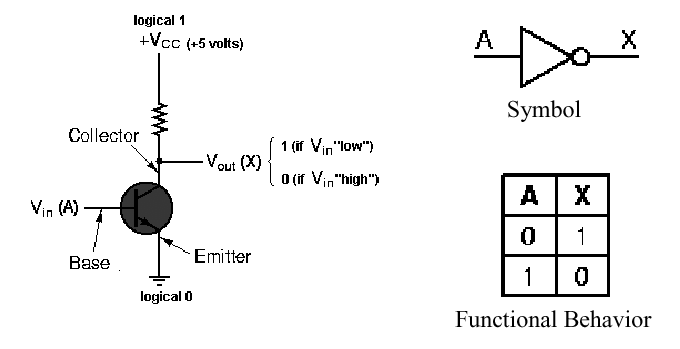
Figure 1.15. Transistor implementation of a NOT gate, adapted from [Maf01].
1.4.3.2. NAND Gate Circuit. The nand
gate is implemented using the operating principle of the not
circuit shown in Figure 15. As shown in Figure 1.16, if both
transistors have a high input (A = 1 and B = 1), then both transistors
conduct, and Vcc is grounded. This produces little or no
voltage drop from the voltage supply to ground, and near-zero voltage
(logical zero value) occurs at the gate's output. This implements the
entry for zero output in the nand gate's truth table, shown
again in Figure 1.16 for purposes of verification.
If either (or both) input(s) of the nand
circuit shown in Figure 1.16 is (are) low, then the two transistors
taken together do not form a conducting path, and there is a
significant voltage drop (logical one) at the gate output. This
implements the nonzero entries of the nand gate's truth table.
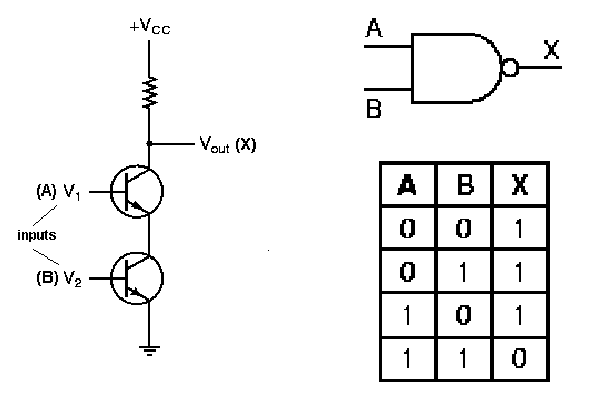
Figure 1.16. Transistor implementation of a NAND gate, adapted from [Maf01].
1.4.3.3. NOR Gate Circuit. The nor
gate is implemented using the operating principle of the not
circuit shown in Figure 15. As shown in Figure 17, if both
transistors have a low input (A = 0 and B = 0), then both transistors
do not conduct, and Vcc cannot be grounded. This produces a
significant voltage drop from the voltage supply to ground, and a
logical one value occurs at the gate's output. This implements the
sole entry for unitary output in the nor gate's truth table, shown
again in Figure 17 for purposes of verification.
Conversely, if either (or both) input(s) of the nand
circuit shown in Figure 1.16 is (are) high, then either (both) transistor(s)
form a conducting path that grounds Vcc, yielding no
significant voltage drop (logical zero) at the gate output. This
implements the zero entries of the nor gate's truth table.
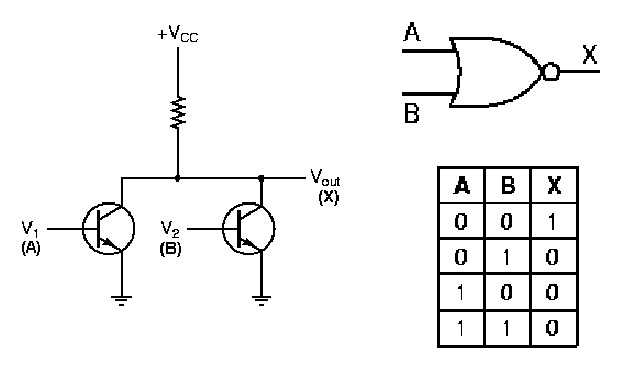
Figure 1.17. Transistor implementation of a NOR gate, adapted from [Maf01].
Integrated circuits often contain multiple gates in
one in-line package. For example, the layout of a quad nand
gate IC is shown in Figure 1.18. Note that the notch in the
circuit packaging material, shown on the left-hand side of the IC,
helps orient the IC user to the pin ordering scheme. Each nand
gate input and output pin is unique, with a pin for the common supply
voltage Vcc, and another pin for common ground.
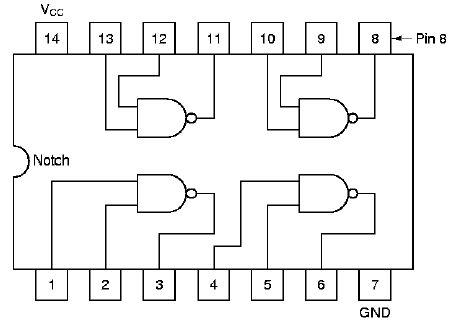
Figure 1.18. Example of quad nand gate integrated circuit pin-out diagram, adapted from [Maf01].
We next examine how the laws of Boolean algebra
can be used to generate designs for more complicated logic circuits.
1.4.4. More Complex Logic Circuits
In this section, we present several examples of how
complex logic circuits can be designed from equations that represent
the circuit's functionality, or from truth tables.
1.4.4.1. Laws of Boolean Algebra. Each type of
formal logic has rules for manipulating operations and operands. In
Boolean algebra, the following rules hold:
Assumption. Let B = {0,1}, with
p,q,r 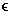 B and
x,y,z
B and
x,y,z 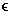 R. This
assumption will hold for the subsequent discussion.
R. This
assumption will hold for the subsequent discussion.
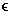 B and
x,y,z
B and
x,y,z 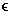 R. This
assumption will hold for the subsequent discussion.
R. This
assumption will hold for the subsequent discussion.
Identity. In arithmetic with real numbers, x
· 1 = x and x + 0 = x. In logic, the analogous
statements are
p and 1  p,
and p or 0
p,
and p or 0  p .
p .
 p,
and p or 0
p,
and p or 0  p .
p .
Domination. In arithmetic with real numbers,
x · 0 = 0. The logical analogue is
p and 0  0 .
0 .
 0 .
0 .
Symmetrically, p or 1  1 .
1 .
 1 .
1 .
Idempotency. This property can be used to
simplify and or or operations, i.e.,
p or p  p
p
p and p p .
p .
 p
pp and p
 p .
p .
Double Negation. In arithmetic, -(-x) = x.
In logic,
not(not(p))  p.
p.
 p.
p.
Commutativity. In arithmetic, addition and
multiplication are commutative, i.e., x + y = y + x and x
· y = y · x. In logic, we have analogous
formulations:
p or q  q or p
q or p
p and q q and p .
q and p .
 q or p
q or p p and q
 q and p .
q and p .
Associativity. In arithmetic, addition and
multiplication are associative, i.e., (x + y)+ z = x + (y +
z) and (x · y) · z = x · (y · z). In logic,
we have the analogous formulations:
(p or q) or r  p or (q or r)
p or (q or r)
(p and q) and r p and (q and r) .
p and (q and r) .
 p or (q or r)
p or (q or r) (p and q) and r
 p and (q and r) .
p and (q and r) .
Distributivity. In arithmetic, multiplication
distributes over addition. In logic, we have a similar
situation:
p and (q or r)  (p and q) or (p and r)
(p and q) or (p and r)
p or (q and r) (p or q) and (p or r) .
(p or q) and (p or r) .
 (p and q) or (p and r)
(p and q) or (p and r) p or (q and r)
 (p or q) and (p or r) .
(p or q) and (p or r) .
DeMorgan's Laws. Manipulation of logical
statements is greatly aided by DeMorgan's laws, which
describe a property that resembles distributivity:
not(p or q)  not(p) and not(q)
not(p) and not(q)
not(p and q) not(p) or not(q) .
not(p) or not(q) .
 not(p) and not(q)
not(p) and not(q) not(p and q)
 not(p) or not(q) .
not(p) or not(q) . Self-Exercise. Construct truth tables for (a) distributive and (b) DeMorgan's Laws, listed above.
1.4.4.2. Circuit Equivalence. Using the
preceding equivalences, especially DeMorgan's laws, it is possible to
transform one circuit form (e.g., nor logic) into another form
(e.g., nand logic). Here, nor logic uses nor gates,
and symmetrically for nand logic.
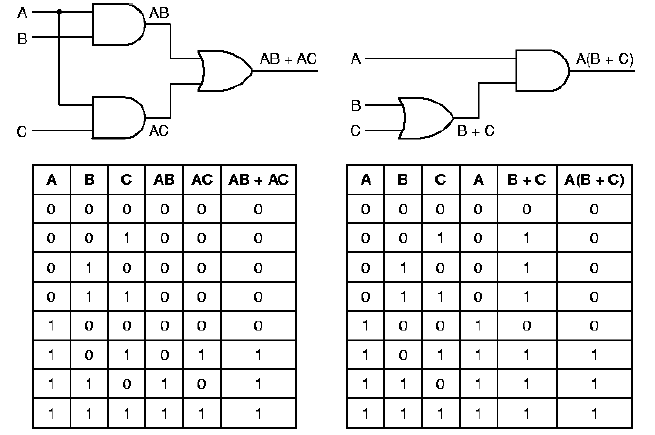
Figure 1.19. Example of quad nand gate integrated circuit pin-out diagram, adapted from [Maf01].
For example, Figure 1.19 shows a circuit that outputs a
one when inputs A and C are both one, or when A and B are both one, and
outputs a zero otherwise. Note that the left-hand circuit has the same
truth table as the right-hand circuit. Also note that the circuit
equation for the left-hand circuit (AC + AB) can be rewritten using
the distributive law (from Section 1.4.4.1) to yield A(C+B),
which is the equation for the right-hand circuit. Here, the minterm
AC means (A and C), and the minterm C + B means
(C or B).
Logic transformations are primarily used for circuit
minimization. For example, Note that the right-hand circuit in Figure
1.19 has only two gates, while the left-hand circuit uses three gates.
This is because the expression AC + AB requires three operations (two
and, one or), while the expression A(C + B) requires
two operations (one and, one or).
1.4.4.3. Majority-Vote Circuit. Given N inputs
a1, a2, ..., aN, the majority vote
function outputs a one when N/2 or more of the inputs are ones, and
zero otherwise. (If N is odd, then N/2 is rounded up to the nearest
integer.) Figure 1.20 illustrates a logic circuit that implements
the majority vote function for three inputs. Observe that the inputs
A, B, and C and their negations (represented by a bar above each variable)
are present in buses (vertical lines), then are combined to form
the four minterms listed in the equation for M. Including the not
gates used for negation, eight gates are required to implement this
circuit. Note, however, that the and gates each have three
inputs (corresponding to the three variables in each minterm) and the
or gate that produces the circuit output has four inputs
(corresponding to the four minterms of the equation for M).
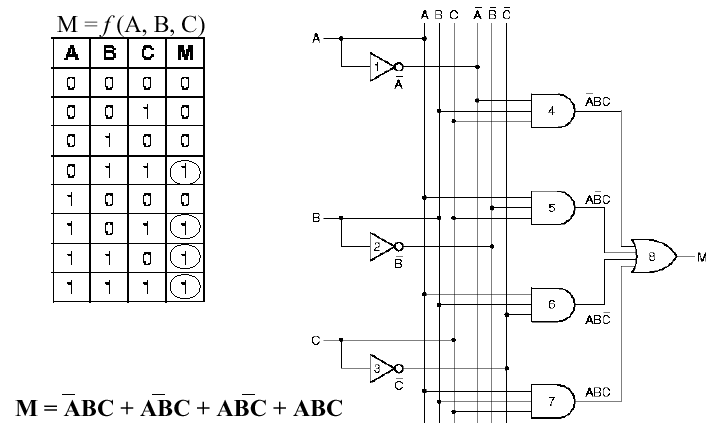
Figure 1.20. Example of Majority Vote Circuit, its truth table, and the governing equation, adapted from [Maf01].
Self-Exercise. How many minterms would there be in the equation for the majority-vote circuit with four inputs? five inputs? N inputs?
1.4.5. Comparators and Combinatorial Logic
Combinatorial logic circuits include multiplexers,
demultiplexers, encoders, decoders, and comparators. A combinatorial
circuit has many inputs and one (or, sometimes, more than one) output.
The output(s) of a combinatorial circuit are uniquely determined by
the inputs. Combinatorial circuits have no memory elements. We will
begin our discussion of combinatorial circuits with the simple example
of a comparator, then progress to the multiplexer and decoder.
1.4.5.1. Comparator. It is often useful to
determine whether or not two operands are equal, which is called
comparison. A digital logic circuit that determines whether or
not two four-bit operands A =
(A0,A1,A2,A3) and B =
(B0,B1,B2,B3) are equal is
shown in Figure 1.20. The algorithm that the circuit implements is
based on the concept of an exclusive-or operation (also called
an xor operation), which is instantiated in an xor gate.
The xor function resembles the inclusive or,
except that when both inputs are high, the xor output is zero,
as shown in the following truth tables:
A B X A B X
-+--------------- -+---------------
xor | 0 0 0 or | 0 0 0
| 0 1 1 | 0 1 1
| 1 0 1 | 1 0 1
| 1 1 0 | 1 1 1
After the xor operation is applied to each bit
of A and B (we call this bitwise processing), the xor
outputs are operated on by a quad-input nor gate. Thus, if any
of the bits are different, the or part of the nor gate
will return a one, and the not part of the nor gate will
return a zero. If A0 = B0 and
A1 = B1 and A2 = B2
and A3 = B3, then the nor gate
will applu the or operation to the outputs of the xor
gates (which will all be one) to yield a one, which will be inverted
at the output of the nor gate to yield a zero.
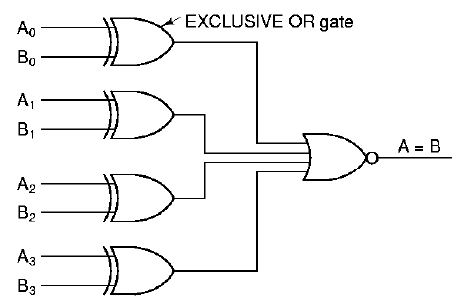
Figure 1.21. Example of Comparator Circuit, adapted from [Maf01].
1.4.5.2. Multiplexer. A multiplexer has
n control signals and 2n inputs (sometimes
called data lines). The purpose of a multiplexer is to use the
control signals to decide which of the inputs will be routed to the
multiplexer's output. Thus, the multiplexer is a type of switching
device that chooses its output from among its inputs, based on control
signals.
For example, Figure 1.22 illustrates a multiplexer
with n = 2 control lines (A, B) and 2n inputs
(D0 through D3). Note that inverters (not
gates) provide the complement of A and B for constructing the minterms
of the circuit's governing equation.
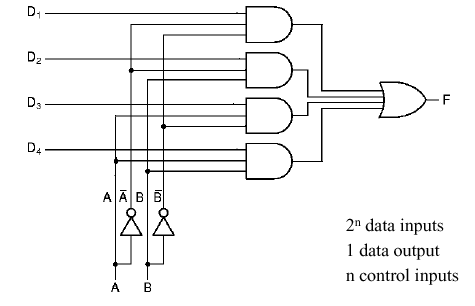
Figure 1.22. Example of Multiplexer Circuit, adapted from [Maf01].
Self-Exercise. Write the governing equation of the multiplexer shown in Figure 1.22. How does this compare with the governing equation of the majority-vote circuit shown in Figure 1.20? In what detailed ways are these circuits different?
1.4.5.3. Decoder. A decoder can be loosely
thought of as a kind of reverse multiplexer, without the control lines.
A decoder has n inputs, and 2n outputs. The
input indexes the output - for example, if the input is 000,
then the output D0 will be high. If the input is 001,
(or 010) then the output D1 (resp. D2) will be high,
and so forth.
For example, Figure 1.23 illustrates a decoder
with n = 3 inputs (A, B, C) and 2n = 8 outputs
(D0 through D7). As in the multiplexer circuit,
inverters provide the input complements for constructing the minterms
of the circuit's governing equation.
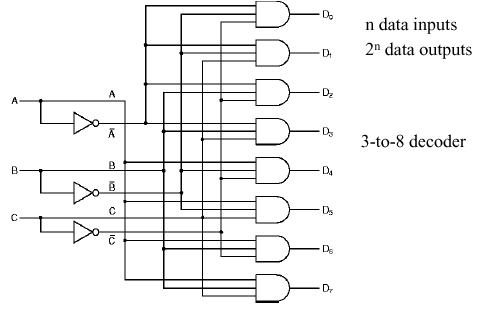
Figure 1.23. Example of Decoder Circuit, adapted from [Maf01].
Self-Exercise. Write the governing equation of the decoder shown in Figure 1.23. How does this compare with the governing equation of the multiplexer shown in Figure 1.22? In what detailed ways are these circuits different? (Hint: Think about minterms, complementation, and DeMorgan's laws.)
Thus, decoders can be used to select one object from
a large number of indexed objects, given a Boolean representation of
the index of that object at the decoder's input. For example, if the
decoder outputs each control a relay that switches a voltage through a
different resistor value, then it is possible to construct an
n-to-2n decoder that converts an n-bit
input signal into an analog voltage ranging from zero to
2n units. However, the circuitry for large n
can become prohibitive, so this technique is of pedagogic interest only.
1.4.6. Programmable Logic Arrays
It is readily seen that circuits such as those shown
in Section 1.4.5 can become prohibitively complex, large, and
power-consumptive if implemented on a circuit board with many chips
containing various types of logic gates. Thus, it is reasonable to
ask how we might put a complex digital circuit on a chip. There are
two ways to do this. First, the circuit can be custom-fabricated,
which is very expensive, especially for small quantities. Second,
one can use programmable logic, which provides many different
types of gates on a chip, with a programmable network of interconnects
between the gates. Programmable logic has widespread software support,
so it is relatively easy (using modern design tools) to design a circuit,
reduce it to a logic schematic (diagram of connectivity and parameters
of logic elements in a circuit), then use a computer to program a
special logic device called a PLA (programmable logic array).
In Figure 1.24, we illustrate a simple PLA circuit.
This type of circuit is called two-level logic because there
are two levels of processing (i.e., and gates at Level 1,
or gates at Level 2).
Self-Exercise. What are the two levels of processing in the circuits shown in Section 1.4.5?
In practice, programmable logic devices are made in a
variety of gate configurations, connectivity networks, and gate
densities. One of the more important types of PLAs is called FPGA,
for
Field Programmable Gate Array. FPGAs represent a new
method of designing custom ICs. Unlike conventionals Gate Arrys, FPGAs
can be designed and programmed by a computer user (e.g., a hardware
designer), and represent an advanced stage of evolution from
Programmable Logic Devices (PLD). FPGAs are advantageous because they
have a much higher gate density than PLAs or PLDs, and offer greater
flexibility. FPGAs are useful for rapid prototyping, especially of
large or complex circuits. Designs can be described using
(a) schematic layout tools, (b) synthesis from a hardware description
language model, or (c) high-level language driven synthesis tools.
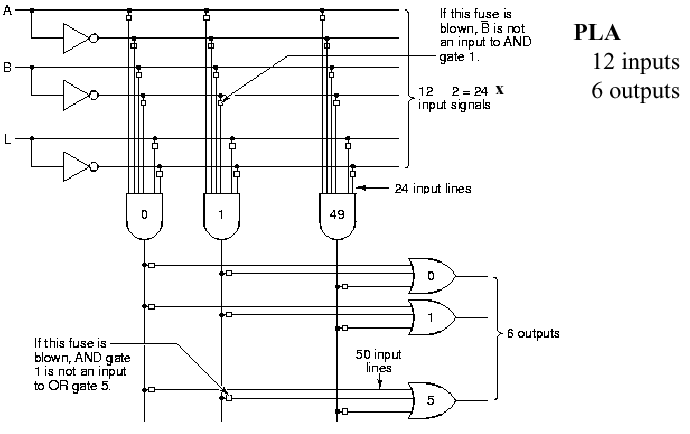
Figure 1.24. Example of programmable logic array, adapted from [Maf01].
The circuit shown in Figure 1.24 is a fused-link
circuit. To program this circuit, a software-driven programming
device merely applies a large voltage to open-circuit (or "blow") each
of the fuses (small boxes in Figure 1.24) that control access to a
given input of a specific gate. For example, if the fuse at the
junction of and gate #1 output and or gate #5 input is
blown, then the and gate output cannot is not an input to that
or gate.
There is a paper on the Web on
Design of High Speed, Low Powered Dynamic Programmable Logic Arrays
that is useful for advanced reading in this interesting topical area.
We next discuss clocked logic circuits.
1.4.7. Synchronous Logic
Thus far, we have considered only asynchronous logic
circuits, in which the input pulses are allowed to propagate through
the circuit at their own speed. This is acceptable for simple logic
designs, but has the disadvantage that one needs to wait a short (usually
somewhat indeterminate) time for the circuit output to stabilize. In
time-critical applications where timing precision is required, the
asynchronous approach to circuit design and implementation does not always
produce useful results, due to indeterminacies in the output settling time.
To remedy this problem, synchronous logic circuits
have been developed whose transition from one state to another is mediated
by a clock pulse. (This can be thought of like people in a band
playing in time to the conductor.) The vast majority of logic circuits
use edge triggered clocking, which means that the state change in
a circuit (e.g., from State Element 1 to State Element 2 in Figure 1.25a)
occurs only when the clock pulse changes from a zero value to a one.
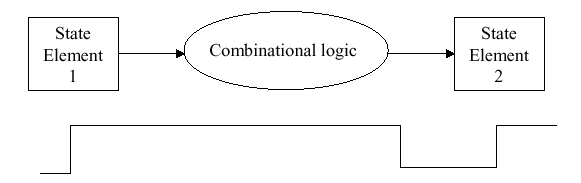
(a)
(b)
Figure 1.25. State changes in logic circuits: (a) synchronous logic changes state on the leading clock pulse (0-1 transition), and (b) asynchronous logic does not require a clock to change state - adapted from [Maf01].
To better understand synchronous logic, which is the
dominant form in digital computing, we next examine how a clock works.
We then discuss latches and storage circuits such as clocked latches
and flip-flops.
1.4.7.1. Principles of the Clock. When we think
of a digital clock, the image of a numerical timekeeping device comes
to mind. However, in digital logic, a clock is really a very precise
oscillator that changes its output from zero to one, then back to zero
in a regular, predictable way.
For example, in Figure 1.26, a clock is comprised of
an oscillator whose output is thresholded to form a train of rectangular
pulses, called a square wave. The clock period is measured
from one 0-1 transition to the next 0-1 transition. The addition of a
delaying device after the clock output causes phase lag between
the clock signals C1 and C2.
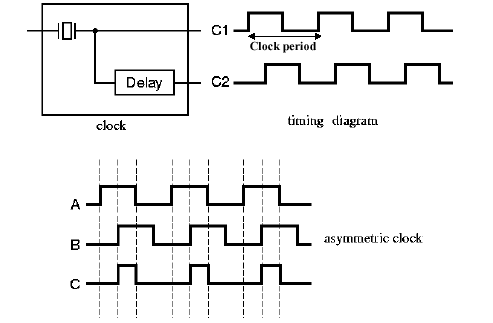
Figure 1.26. Example of clock output, with symmetric (A) and asymmetric (B and C) clock pulses, adapted from [Maf01].
Within a clock cycle, there is the time a pulse is
high (tH) and the time it is low (tL). If
tH does not equal tL within a small measurement
error, then we say that the clock pulse is asymmetric.
This term also holds for a phase-shifted pulse, as shown in signal
B of Figure 1.26.
If tH< tL within a small
measurement error, then we say that the pulse duty cycle is less
than one. This case is shown in Figure 1.26, for the clock signal
labelled C. If tH > tL within a small
measurement error, then we say that the pulse duty cycle is greater
than one.
1.4.7.2. The SR Latch. Early in computing
practice, it was desirable to store a bit in a small memory device.
Since the only usable storage devices were relays (an
electromechanical device) and delay lines that used the metal Mercury
(chemical symbol Hg), it was decided to adapt asynchronous relay-based
logic (very slow) to produce a storage element that could hold one
bit.
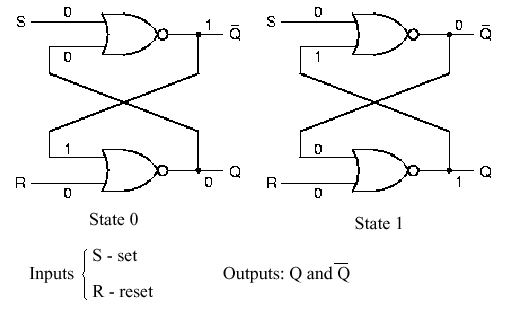
Figure 1.27. The two states of the SR latch, adapted from [Maf01].
Figure 1.27 shows a modern version of this concept,
called the SR Latch, which is implemented in nor logic.
(Using DeMorgan's Laws, it is possible to implement this in
nand logic.) When the Set input is high and the Reset input is
low, State 1 results, and conversely for State 0. Thus, the Set
(Reset) puts a 1 (0) value at the output Q. It is not difficult to
see that placing this circuit after an oscillator could product the
clock pulses shown in Figure 1.26.
Self-Exercise. Derive the truth tables for State 0 and State 1 of the SR latch shown in Figure 1.27.
1.4.7.3. Clocked Latches. The problems with
the asynchronous SR Latch shown in Figure 1.27 are (a) the S and
R inputs can be energized at any time, and (b) settling of the
circuit to yield its output value occurs immediately after the
S or R signals are provided. This situation is remedied in the
Clocked SR Latch of Figure 1.28, where two and gates are
used in conjunction with a clock to drive the SR Latch of Figure 1.27.
The circuit works the same as the SR Latch, with the
following important exceptions. First, if S or R are one, and the
clock value is zero, then the output of the and gates is zero.
If S or R equals one, and the clock is high, then the S,R values are
passed to the input of the SR latch, but only while the clock is high.
This gives the latch time tH to settle (see Section 1.4.7.1).
If S or R are zero, then it doesn't matter what the value of the clock
is - the inputs to the SR Latch remain zero.
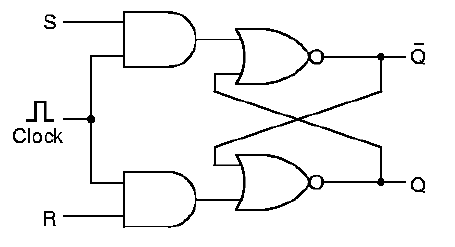
Figure 1.28. The Clocked SR Latch, adapted from [Maf01].
Self-Exercise. (1) Derive the truth table for the clocked input to the SR Latch in Figure 1.28, using the and gate logic, as shown. (2) Prove (using truth tables) how this could or could not be implemented in nor logic.
A problem with the clocked SR latch is that it has
two inputs, and they have a forbidden configuration. Namely,
one cannot apply both S = 1 and R = 1 to the circuit simultaneously -
it won't know which state to enter! This problem is resolved with
the Clocked D Latch, which is a minor variation on the clocked
SR latch.
As shown in Figure 1.29, the D latch adds a not
gate or inverter to the input of the clocked SR latch, so that its "S"
and "R" inputs always have opposite values. In order to avoid confusion
with the SR latch, the input is called D. The clock
pulse is applied to the input, as it was with the SR latch.

Figure 1.29. The Clocked D Latch, adapted from [Maf01].
As shown in Figure 1.29, the D latch has the following
timing behavior (from the D,C,Q signals below the latch circuit).
The D signal is the input (data), C is the clock, and Q is the output.
When D goes high (0-1 transition), nothing happens to the latch until
C goes high. (If D is low by the time C goes high, then the latch does
not change state.)
If D is high and C goes high, then the latch changes
state. There is a slight delay from the time C goes high to the time
Q goes high, which is called the propagation delay (a function
of the type of logic used, the semiconductor fabrication technique,
wire lengths, etc.) When C goes low, whether or not D is high, the
latch output (Q) stays high. This is the memory function of the
SR latch that we discussed earlier. However, if D is low, then if
C goes high (0-1 transition), Q goes low after the propagation delay
occurs. Thus, the D latch only stores a unitary input (D = 1) for
a time equal to the period of the clock. This can be verified by
inspecting the timing diagram in Figure 1.29.
1.4.7.4. The D Flip-Flop. In order to make
the D latch store a value throughout the high state of the clock,
it is necessary to make a more complex circuit using the D latch,
which we call a D flip-flop. The flip-flop is so named because
it can be toggled back and forth between two states (Q = 0 and Q = 1)
by varying D. The D flip-flop is comprised of two D latches and an
inverter, as shown in Figure 1.30
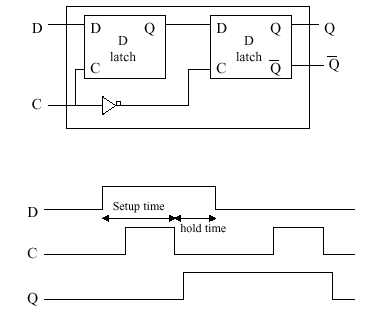
Figure 1.30. The D flip-flop with timing diagram, adapted from [Maf01].
Per Figure 1.30 the D flip-flop has the
following timing behavior (determined from the D,C,Q signals
below the latch circuit). When D goes high (0-1 transition),
nothing happens to the latch until C goes high. (If D is low by the
time C goes high, then the latch does not change state.) At the
trailing edge of the clock pulse (1-0 transition), Q goes high if
it was previously low. If Q was previously high, nothing happens
to Q. When D goes low, nothing happens to Q until the
clock pulse goes low. Then, after a propagation delay, Q goes low.
There are two critical time intervals associated with
the D flip-flop. The setup time is the time required to keep D
high, in order to wait for the trailing edge of the clock pulse. The
hold time is the time required to hold D high after setup, to
ensure that Q stays high.
Self-Exercise. (1) Derive the truth table for each of the four input states of the D flip-flop as shown in Figure 1.30. Hint: Input states are defined by the values of D and C (e.g., State 0: D = 0, C = 0->0; State 2: D = 0, C = 0 -> 1; etc.)
1.5. Computer Performance Assessment
Reading Assignments and Exercises
When we talk about computer performance, we
need to consider the following issues:
- Method of Performance Evaluation - By what measures will the performance be assessed? Will the assessment be local to a specific part of the computer hardware, or global (i.e., across all hardware and software modules)? What will the mix of instructions be?
- Limitations of Evaluation - What are the shortcomings of each method or measure of performance assessment? From whence do these limitations arise, and why? What can be done to improve these limitations?
- Metrics - What formal measures are to be used for performance evaluation? Speed? Time used in a computation? Memory space required?
- Processor Performance Equation - How will the processor's performance be described mathematically? Does the equation portray actual parameters of practical interest, or does the computational model described by the equation not match the processing architecture under test?
- Performance Evaluation Reports - What methods of analysis and presentation are used to evaluate data? Is the data normalized to a particular benchmark result or parameter? Is the normalization performed in a physically meaningful way?
- Ahmdahl's Law - Whatever measurements are made, as one continues to enhance processor performance, the overall improvement achieves diminishing returns.
We examine each of thise issues, as follows.
1.5.1. Performance Evaluation
Computer performance evaluation is primarily based on
throughput and response time. Throughput is how many
bits of data are processed, or how many operations are performed, in a
given interval of time. For example, we say that a processor has a
throughput of N MB/s (megabytes per second). With respect to
execution time of a program on a processor X, we say that
PerformanceX = 1 / Execution TimeX
and, for two processors X and Y,
Relative Performance = PerformanceX / PerformanceY
For example, in the preceding equation, if processor
X is faster than processor Y, then Execution TimeX <
Execution TimeY (all other things being equal), so Relative
Performance < 1. This also implies increased throughput of
X with respect to Y.
Key Concept. As a result, we want to
improve performance by increasing performance, which
means decreasing execution time. In practice, this can be
done by (a) decreasing response time, or (b) adding more processors
to a system (provided I/O is managed efficiently).
1.5.2. Measuring Performance
A program that is executing, or has been executed, has
the following components:
- Wall-Clock Time - how long it takes (typically, time in seconds) for your program to execute, from the time it is invoked to the time it completes. This time is measured with respect to a global time standard, so we name it according to a common object such as a wall clock. This is also called elapsed time.
- CPU Time - comprised of user CPU time (time spent computing the program), and system CPU time (the time the operating system spends supporting the program).
- I/O Time - time spend reading and writing data from/to memory.
- Other Time - time spend running other programs, waiting for the operating system to be scheduled, etc.
We can measure a program's execution time using the
UNIX
time command. For example, let's enter the UNIX
command time du at one's root directory (which can be
reached via the command cd. When I tried this on my
(large) directory tree, I got the following result:
0.21u 1.54s 0:24.49 7.1%
These four numbers have the following meaning:
- User CPU Time = 0.21 seconds, the first number (
0.21u). - System CPU Time = 1.54 seconds, the second number (
1.54s). - Elapsed Time = 24.49 seconds, the third number (
0:24.49). - CPU Activity as Percent of Elapsed Time = 7.1 percent, the fourth number (
7.1%).
Observe that percent CPU activity is computed
as follows:
- Step 1. Add the User and System CPU Times to get Total
CPU Time (e.g., 1.75 sec = 0.21 sec + 1.54 sec).
Step 2. Divide the Total CPU Time by Elapsed Time (e.g.,
0.071 = 1.75 sec / 24.49 sec).
Step 3. Multiply by 100 to get percent (e.g., 7.1% = 0.071 x 100 percent).
Other Time is computed as follows:
- Step 1. Add the User and System CPU Times to get Total
CPU Time (e.g., 1.75 sec = 0.21 sec + 1.54 sec).
Step 2. Subtract the Total CPU Time from Elapsed Time (e.g.,
Other Time = 22.74 sec = 24.49 sec - 1.75 sec).
Given a method of measuring time, and computation of
different times (e.g., CPU, Other) from these measures of time, we can
now discuss a simple model of computation for measuring CPU
performance.
1.5.3. CPU Performance Equation
In order to measure CPU performance in a physically
realistic way, we need a model of computation. In the simplest
case, we start with the number of CPU cycles, defined as follows:
Ncyc = IC · CPI ,
where IC denotes the instruction count (number of
instructions per program), and CPI denotes the average cycles per
instruction.
Given the CPU cycle time tcyc or the
clock rate BWclk, we can express the CPU time as:
tcpu = Ncyc · tcyc
or
tcpu = Ncyc · BWclk .
Patterson and Hennesey [Pat98] express this as

If there are different types or classes of
instructions in a given program, then the preceding equation for
Ncyc is not an accurate estimate, because CPI can be
affected by the instruction mix (nimber of each of type of instruction
that occurs in the program). Thus, we use the following equation to
more accurately determine the number of cycles incurred when a program
is executed:
Ncyc = 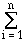 CPIi · ICi ,
CPIi · ICi ,
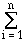 CPIi · ICi ,
CPIi · ICi ,
where we assume that there are n classes of
instructions. The frequency distribution of instructions, which is
comprised of (IC1, IC2, ..., ICn),
is obtained by a technique called execution profiling, which
is supported by a variety of commercial software tools. The number
of cycles per instruction type is determined from analysis of a
specific processor design, validated by performance measurement.
Example 1. To illustrate the practical
utility of these
measurements, let us assume that a program runs in 10 seconds on a
processor with a 400 MHz clock rate. We want to build a new computer
that can
run the program in 6 seconds by increasing the clock frequency
to X MHz. An unfortunate consequence is that the average
CPI will be 1.2 times higher in the new processor. Here's how we set
the problem up to determine the new clock rate X:
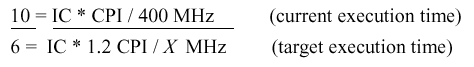
Solving the equation yields X = 800 MHz. Thus,
we see that doubling the clock rate does not necessarily double the
processor speed, because there are other variables (e.g., CPI or
the instruction mix) that can be affected, as shown below.
Example 2. Now we will consider the effect of
instruction mix. Assume that the following data are correct:
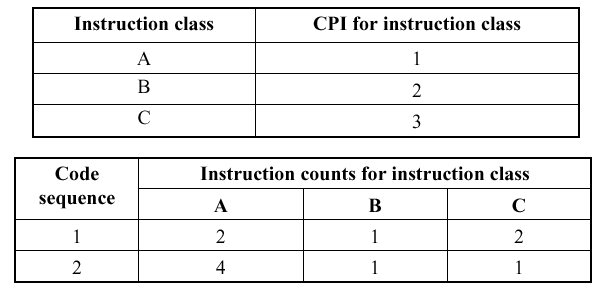
Q: Which code sequence will be faster - #1 or #2?
A: The sequence that incurs the least number
of cycles is faster. Using the preceding equation for Ncyc
we see that the number of cycles for code sequences 1 and 2 are given
by:
Ncyc(Seq.1) = (2 · 1) + (1 · 2) + (2 · 3)
= 10 cycles
Ncyc(Seq.2) = (4 · 1) + (1 · 2) + (1 · 3) = 9 cycles .
Ncyc(Seq.2) = (4 · 1) + (1 · 2) + (1 · 3) = 9 cycles .
Thus, code sequence #2 is faster, because it requires
9 cycles, versus 10 cycles for code sequence #1.
1.5.4. Performance Evaluation
In an ideal situation, one has a suite of programs
whose instruction mix is known exactly. By running each program on
a processor to be analyzed, it is possible to determine CPI for each
type of instruction. However, life is rarely ideal. Thus, we have
the following types of benchmarking programs to measure and
bound processor performance:
- Synthetic Benchmarks are used to exactly measure specific characteristics of a processor (e.g., memory I/O performance, register-to-register I/O, speed of arithmetic functions, etc.) Because the benchmarking program is synthetic, one can put any combination of instructions into it, and the benchmark is not necessarily realistic.
- Toy Benchmarks are simple but somewhat realistic programs that help the designer get a preliminary idea of a how a processor will behave under pseudo-realistic constraints. These might include tasks such as solving a simple matrix equation, performing a near-trivial image processing operation, etc.
- Kernels are more involved programs that capture the functionality of a larger program. For example, one can use an operating system kernal to get an idea of the operating system performance on a given processor, provided that the kernal is executed significantly more in practice than the other programs in the operating system.
- Real programs are used (a) to measure performance at many stages of processor design, (b) to estimate the processor's performance under realistic computing constraints and (c) in assessment of fielded systems.
In practice, realistic benchmarks include engineering
or scientific applications, software development tools, transaction
processing, and office applications such as large spreadsheets or
formatting of word processing documents.
1.5.5. Performance Reporting
After one has measured the performance of a given
processor, then one formulates a test report. In order to
make our report accurate and meaningful to a hardware designer,
we must have at least three elements in the report:
- Hardware/Software Configuration tells the designer what benchmarking programs were run on the processor under test, and how the processor was set up (e.g., how much memory, what clock rate, compiler version, etc.)
- Evaluation Process Conditions provide information about special constraints on the instruction mix that can influence the reproducibility of the performance measurement.
- Performance Summary is typically expressed in terms of average rates. How these averages are computed is of practical interest.
For example, consider the following types of means:
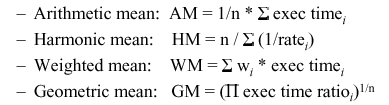
Normalized results are not easily understood or
accurately compared with the arithmetic mean, because the mean of
ratios between two series of measurements is not the same as the ratio
of the series means. Instead, normalized results should be combined
with the geometric mean, which is independent of the data series used
for normalization. This is because the ratio of two series' geometric
means is the same as the mean of the ratios between the series.
That is, given two data series {Ai} and
{Bi}, where i = 1..n, if the arithmetic mean is used, then
AM({Ai}) / AM({Bi}) 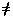 AM({Ai / Bi})
AM({Ai / Bi})
whereas, with the geometric mean:
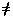 AM({Ai / Bi})
AM({Ai / Bi})
GM({Ai}) / GM({Bi}) =
GM({Ai / Bi}) .
Here, the construct {Ai / Bi}
means divide the i-th element of A by the i-th element of B.
For example, if {Ai} = {2,4,6} and {Bi} =
{2,2,3}, then {Ai / Bi} = {2/2, 4/2, 6/3} =
{1,2,2}.
Example. The practical implications of this problem are
illustrated in the following table:

Here, "Normalized to A" means that the data for
processors A, B, and C are divided by the data for A. In the first
set, programs P1 and P2 are both normalized to A, hence, the
arithmetic and geometric means for A are both 1.0 (the mean of 1.0 and
1.0 is 1.0). However, the arithmetic mean for B is 5.05 = (10.0 + 0.1)/2,
while the geometric mean for B is 1.0, due to the previously-mentioned
normalization property. Total execution time is likewise normalized
in the first set, to the value for A, which is 1001 = 1000 + 1. Thus,
the total time for B = 0.10989 = (100 + 10) / 1001, which is approximately
0.11.
Self-Exercise. (1) Derive all the entries in the preceding table. Be able to explain how each one was calculated. (A problem like this will likely be an exam question.)
1.5.6 Implications of Amdahl's Law
In the 1960s, Gene Amdahl derived an equation that
expresses the diminishing returns that one obtains when trying to
optimize a computer program. His equation has been adapted by
Patterson and Hennesey, as follows:
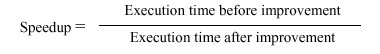
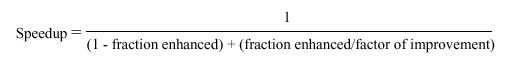
This means that, the more you enhance the performance
of a fraction f of a program or processor, the remaining
(unenhanced) part (1 - f) gets progressively smaller. In order
to keep the speedup S constant for each enhancement, you have to
enhance performance of the remaining (1 - f) part to have a much
greater speedup than S.
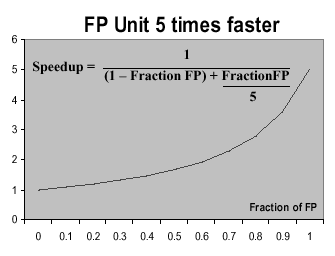
Example. Suppose a program takes 10 seconds to
execute on processor P. After P's floating point (FP) unit is enhanced
to be 5 times faster, then reinstalled in P, the effective speedup
is graphed in Figure 1.31a. Here, the speedup is on the ordinate
(vertical axis) and the fraction of the execution affected by the FP
is on the abscissa. What is obvious is that in order to obtain a
speedup of 2.0, the new FP has to be used approximately 0.65 (65
percent) of the time. In all but the most highly parallelized image
or signal processing code, this is quite unlikely.
(a)
(b)
Figure 1.31. Amdahl's Law applied to processor performance enhancement, adapted from [Maf01].
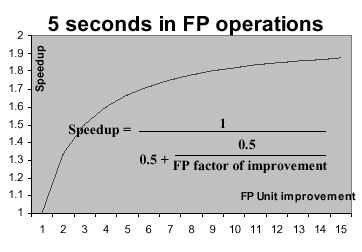
The situation worsens in Figure 1.31b. Here, we see
that if the new FP unit affects only 1/2 of the program execution,
then we will approach a speedup of 2.0 asymptotically, regardless of
how much the FP unit's performance is improved. As in Figure 1.31a,
the speedup is graphed on the ordinate, with the enhancement factor of
the FP unit on the abscissa.
Amdahl's Law has important implications for practical
computer design. Namely, if a portion of the CPU does not affect
program execution very much, then there is little point in drastically
enhancing its performance. As a result, we try to enhance the most
frequent deficiencies first. This is called enhancing the common
case and it works, for the reasons shown in the preceding example.
1.6. Performance Benchmarking
Reading Assignments and Exercises
As we discussed in Section 1.5, a benchmark is
a program that is used to measure a computer system's performance in a
more-or-less standardized way. We aspire to standard benchmarks
because of the need for realism and reproducibility in performance
testing. In the ideal situation, one can test a processor using a
representative sample of real workload. In practice, one first
characterizes the working set of programs statistically (e.g., number
of operations of each type), then computes the time each program requires,
based on the sum of the product CPIi · ICi
over all instruction types.
We next overview different types of benchmarks and
how they have been, or are, used in practice.
1.6.1. Linpack Benchmark
The Linpack benchmark is an old, well-established measure
of CPU and ALU performance that measures the time required to solve a dense
system of linear equations. In FORTRAN, the Linpack kernal resembles the
following loop:
DO 10 I = 1,N
DY(i) = DY(i) + DA * DX(i)
10 CONTINUE
Here, the "D" that precedes each variable denotes a
double-precision operand. As a result, the Linpack benchmark
challenges the ALU and control unit primarily. However, I/O is also
challenged, due to the large data requirement associated with the
vectors DX and DY.
Linpack has the following measures (also called
metrics):
- Rpeak - peak system performance, in Gflops
- Nmax - matrix size that yields the highest Rpeak
- N1/2 - matrix size that yields the 0.5 · Rpeak
- Rmax - Gflops achieved for the matrix of size Nmax
You can read more about the Linpack benchmark at
http://www.top500.org/.
1.6.2. Intel's iCOMP Index 3.0
The iCOMP index is a geometric mean of relative
performance measures (recall from Section 1.5 how geometric means work
well with ratio-based metrics [also called ratiometric
quantities]). The benchmark contains a mix of instructions that
are assumed to characterize existing and emerging software. The iCOMP
benchmark seems to be more relevant as the use of 3D graphics,
multimedia, and Internet access increases.
iCOMP 3.0 has the following composition, with weighting
indicated in percent:
- #1,2: Multimedia and Internet application (25%)
- #3: Two integer productivity applications (20% each)
- #4: 3D geometry and lighting calculations (20%)
- #5: Java application (10%)
- #6: Floating point: engineering, finance, and game applications (5%)
The preceding six benchmark results are combined as
follows. Let the ratio BMi/Base_BMi denote the
i-th benchmark performance, where BM denotes the benchmark run on a
test processor, and Base_BM denotes the benchmark run on a baseline
processor, in this case a Pentium II clocked at 350 MHz. The iCOMP
benchmark is computed as:
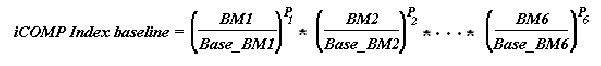
where Pi denotes a weighted exponent that
incorporates the 1/6 power (root) that comprises the outer operation
of the geometric mean. Thus, the iCOMP index is a weighted geometric
mean of application-specific performance ratios.
1.6.3. SPEC2000 Benchmarks
The System Performance Evaluation Corporation (SPEC)
benchmarks are upgraded every 2-3 years, to account for the
characteristics of software as program designs evolve. For example,
longer run time, larger problems, and greater diversity of
applications characterize newer software. The SPEC2000 benchmark has
both baseline and optimized measures, comprised of the geometric mean
of normalized execution times. The reference machine for SPEC2000 is
a Sun Ultra5_10 (300 MHz SPARC architecture with 256MB of memory).
The current SPEC2000 suite is comprised of the
following 12 integer and 14 floating point (FP) programs, which measure
response time and throughput:
164.gzip(C, integer) - Compression175.vpr(C, integer) - FPGA circuit placement and routing176.gcc(C, integer) - C programming language compiler181.mcf(C, integer) - Combinatorial optimization186.crafty(C, integer) - Chess game197.parser(C, integer) - Word/language processing252.eon(C++, integer) - Computer visualization253.perlbmk(C, integer) - PERL programming language254.gap(C, integer ) - Group theory, interpreter255.vortex(C, integer) - Object-oriented database256.bzip2(C, integer ) - Another compression program300.twolf(C, integer ) - Place and route simulator168.wupwise(Fortran-77, FP) - Physics/quantum chromodynamics171.swim(Fortran-77, FP) - Shallow water circulation modelling172.mgrid(Fortran-77, FP) - Multigrid solver: 3D potential field173.applu(Fortran-77, FP) - Parabolic/elliptical PDEs177.mesa(C, FP) - 3D graphics library178.galgel(Fortran-90, FP) - Computational fluid dynamics179.art(C, FP) - Image recognition/neural networks183.equake(C, FP) - Seismic wave propagation simulation187.facerec(Fortran-90, FP) - Image processing: Face recognition188.ammp(C, FP) - Computational chemistry189.lucas(Fortran-90, FP) - Number theory/Primality testing191.mfa3d(Fortran-90, FP) - Finite-element crash simulation200.sixtrack(Fortran-77, FP) - High energy nuclear physics accelerator design301.apsi(Fortran-77, FP) - Meteorology: Pollutant distribution
SPEC2000 metrics derived from the integer benchmarks
(#1-12, above) include:
SPECint2000: The geometric mean of 12 normalized ratios when each benchmark is compiled in highly optimized mode (also called aggressive optimization)SPECint_base2000: The geometric mean of 12 normalized ratios when compiled with normal optimization (also called conservative optimization)SPECint_rate2000: The geometric mean of 12 normalized throughput ratios when compiled with aggressive optimizationSPECint_rate_base2000: The geometric mean of 12 normalized throughput ratios when compiled with conservative optimization
The results of the SPEC2000 integer benchmarks are
shown in Figure 1.32, where the circle denotes the geometric mean, and
the spokes of the wheel whose rim is the circle denote individual
benchmarks keyed positionally to the diagram in the upper left-hand
corner. Note that the Mips processor with IRIX operating system performs
significantly worse than the mean on
181.mcf
(combinatorial optimization), and the three processors all perform
worse than the mean on 255.vortex (object-oriented
database) and 252.eon (computer visualization). Since
databases and visualization involve significant I/O, and visualization
involves significant amounts of graphics, it would be reasonable to
suggest that these areas need improvement in each of the three
processors tested.
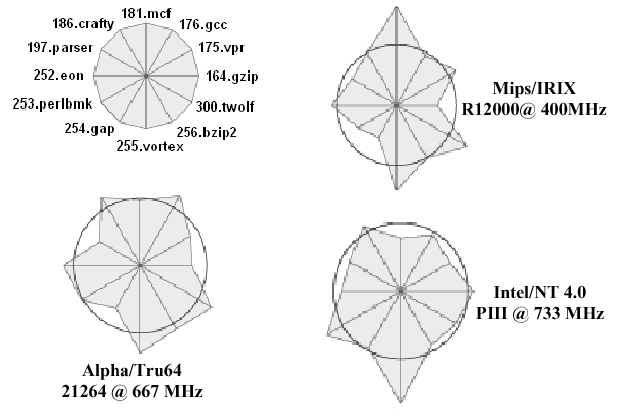
Figure 1.32. Test results for the SPEC2000 integer benchmarks run on three processors, with key in the upper left hand corner, after [Maf01].
The floating-point benchmarks shown in Figure 1.33
reveal similar discrepancies. For example, all processor perform
relatively poorly on the
179.art (neural net) benchmark,
which involves significant amounts of multiplication and division by
small magnitudes. It is interesting to note that, in both the integer
and floating point benchmark suites, the Intel Pentium III processor
appears to have the most uniform performance (largest number of
benchmark results closest to the mean). Since Intel is a contributor
to the SPEC benchmark suite, it is not surprising that their
processors could be designed to perform well on these established
benchmarks.
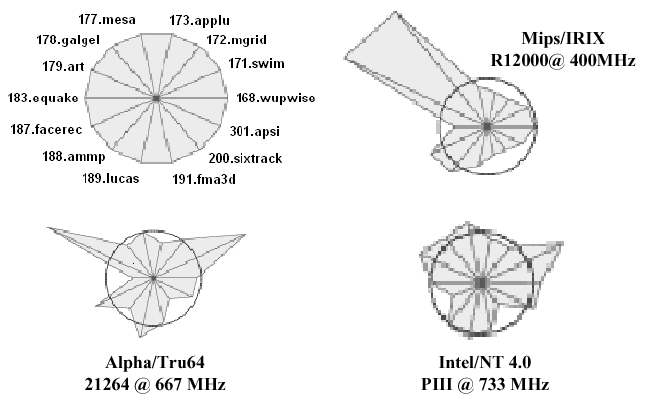
Figure 1.33. Test results for the SPEC2000 floating point benchmarks run on three processors, with key in the upper left hand corner, after [Maf01].
When the geometric means (of the SPEC95 integer
and floating-point benchmarks) are respectively graphed as a function
of clock rate, we have the results shown in Figures 1.34 and 1.35. Note
that (a) SPEC95 is similar to SPEC2000, and (b) the performance of the
Pentium Pro exceeds that of the Pentium due to microarchitecture
improvements.
Figure 1.34. Graph of SPEC95 integer benchmark performance as a function of processor clock rate in MHz, adapted from [Maf01].
It can also be seen that the improvement in performance
carries through to the floating point computations, as shown in Figure
1.35. However, the slope of the floating point benchmark curve for
the Pentium is not as great as that for the integer benchmark. This
could imply (depending on the statistical significance of the measurements)
that the Pentium processor does not yield improvements as readily for
floating point computations as it does for integer computations.
Figure 1.35. Graph of SPEC95 floating point benchmark performance as a function of processor clock rate in MHz, adapted from [Maf01].
1.6.4. MIPS Benchmark
The speed of a processor in millions of instructions
per second (MIPS) can be estimated as:
MIPS = IC / (106 · tcpu) ,
where tcpu denotes CPU time. Unfortunately,
due to different behavior characteristics of various processors (e.g.,
as shown in Figures 1.32 and 1.33) 1 MIPS on a given processor may not
mean the same thing as 1 MIPS on another processor. In particular,
MIPS is based heavily on instruction count (IC). This is like determining
the winner of an auto race by who used fewer RPMs, or the winner of a
marathon by who took fewer steps when running.
In practice, MIPS is especially misleading because
floating point computations are done differently on different systems.
For example, some computers do FP operations in software, while others
use dedicated hardware units on- or off-chip. Also, the MIPS benchmark
does not factor in the instruction mix, and thus compromises realistic
characterization of workload.
The only situation where MIPS might be a useful benchmark
is when the majority of variables have been fixed - for example, when
comparing two processors from the same vendor that support the same
ISA using the same compiler or the same benchmark suite. Apart from
that, MIPS should be avoided as a measure of processor performance.
1.6.5. Fallacies and Pitfalls
When applying benchmarks to processors, one should
avoid making the following mistakes:
- Ignoring Amdahl's Law occurs when one tries to recursively optimize a processor, and puts much effort into the optimization process, only to achieve diminishing returns. Instead, one should optimize the common case first, then determine via a mathematical model such as Amdahl's Law whether or not further optimization is cost-effective.
- Using MIPS as a performance metric is a common mistake, especially when one is in a hurry to portray a processor's performance in a favorable way. Instead, standard or well-established suites of benchmarks (such as the SPEC or iCOMP suite) should be applied to the processor, to highlight performance deficits in several categories.
- Using the Arithmetic Mean of normalized CPU times is erroneous mathematically because the normalized CPU times are ratiometric quantities. As such, they cannot be combined into an ensemble statistic using the Arithmetic Mean. Instead, the Geometric Mean must be employed to combine ratiometric quantities.
- Using "hardware-independent" measures such as code size defeats the purpose of hardware performance testing, namely, to highlight the specific advantages and deficits of a given processor. If the benchmark is hardware-independent, then it cannot produce information that is specific to a given architecture or processor. Instead, a suite of benchmarks such as SPEC or iCOMP should be used to identify hardware-specific performance deficits.
- Assuming that synthetic benchmarks predict real performance is a major but common error. Recall from our discussion in Section 1.5, that synthetic benchmarks are programs devised by algorithm or hardware designers to measure specific types of performance on highly focused types of operation mixes. Because these benchmarks often bear little or no resemblance to real programs, they are of little use in characterizing a processor's performance in practical applications. Instead, a suite of benchmarks that is comprised of practical programs, such as SPEC or iCOMP, should be used.
- Assuming that the geometric mean of CPU time ratios is proportional to the total execution time is erroneous for two reasons. First, the arithmetic mean, which is based on a sum, is proportional to total time. The geometric mean is based on a product and is thus not proportional to an accumulated (summed) total measure. Second, the CPU time is only part of the total execution time. Other factors that influence total time are I/O activity, wait time in a multiprocessor system, and network overhead in a parallel or distributed computing system.
In summary, performance measures are specific to a
given program or suite of programs. CPU time is the only adequate
measure of CPU performance - other metrics, such as I/O time or total
time factor in effects that are not properly associated with the CPU
(although they may be associated with a computer system). For
a given ISA, performance increases result from (a) increases in clock
rate, (b) improvements in processor architecture that reduce CPI, and
(c) compiler enhancements that reduce IC (and, possibly, CPI) for a
given type of instruction. The ideal benchmark is the workload that
you plan to run on a given processor: all other assumptions about
benchmarks can lead to unrealistic performance figures.
No comments:
Post a Comment