1.1. Brief History of Data Compression Applications and Research
Research in signal and image compression has been extensive, due primarily to the economic benefits of exploiting communication channel bandwidth. In principle, compression is achieved by reducing redundancy in the source data. For example, an image of constant value k can be represented by one number (k), regardless of image size. In contrast, an image consisting of randomly chosen pixel values cannot be compressed. Early on, it was recognized that the first derivatives of many signals exhibited lower information content than the source signal [1]. This led to the development of primitive methods of image compression such as delta modulation [5] and differential pulse code modulation (DPCM). As a consequence of the need for accurate, efficient quantizers in PCM and DPCM, a variety of statistical compression techniques were developed including adaptive DPCM, which were based upon recursive or adaptive quantization techniques [6]. As digital images increased in size and thus required higher channel bandwidth and increased storage, data compression research began to emphasize two-dimensional transformations. For example, the concept of subdividing an image into blocks (generally of rectangular shape) gained popularity due in part to the limited memory then available on fast signal processors. Such methods, called block encoding (BE), tessellate the image domain into encoding blocks that exhibit greylevel configurations which can be represented in lossless form (e.g., via indexing) or with a lossy transform such as vector quantization. Since there are fewer block configurations than there are possible blocks, and a group of values are represented by an index or by an exemplar block (also called a vector), VQ produces the desired effect of image compression. By arranging the input data to achieve maximum intra-vector and minimum inter-vector correlation, the compression ratio of VQ can be increased, which partially offsets the effort required by the determination of the VQ codebook, which is a set of exemplar vectors [7].An alternative method of block encoding, called block truncation coding (BTC) [8], encodes regions of low greylevel variance in terms of a mean value and regions of high variance in terms of a mean, standard deviation, and a residual bitmap that denotes the positions of zero crossings. Unfortunately, BTC is expensive computationally, due to the adjustment of bits in the bitmap to effect reduced entropy. Since the cost of BTC increases exponentially with blocksize [1,8], and BTC has a compression ratio that is moderate by today's standards (typically 20:1 to 25:1 for images of natural scenes), BTC is not considered a compression transform of choice.
Additionally, by transforming the output of a block encoder with, for example, the Fourier or Cosine transforms, then selecting transform coefficients that are deemed significant a priori, one can further reduce the image data burden, although at the cost of information loss. Such methods are generally called transform coding [9], and feature prominently in compression schemes (e.g., JPEG, MPEG) that are currently in vogue for digital telephony applications [10]. By following the coefficient selection stage (i.e., quantization step) with a provably optimal, lossless compression transform such as Huffman encoding [11], one can obtain further data reduction and thus achieve higher compression ratios without incurring information loss.
More exotic methods of image coding are based upon the reduction of an image to significant eigenvalues, as in the Singular Value Decomposition (SVD) [12]. Although proven optimal for image compression, eigenvalue transforms such as the SVD and Karhunen-Loeve transform (KLT) are computationally burdensome, requiring O(N4) work for an NxN-pixel image. Thus, the SVD and KLT are infrequently employed, despite the mathematical simplicity of obtaining significant transform coefficients (eigenvalues) from the transformed image.
An alternative method of compression by recursive decomposition, which is often based upon knowledge derived from observation of the human visual system (HVS), has been employed with some success but tends to be data-dependent. For example, early attempts at multifrequency decomposition, such as the Synthetic High technique [9], eventually led to Fourier-transform based methods currently known as wavelet based compression [13]. Similarly, Barnsley et al. [14,15] have published extensively in the area of image compression based on recursive, VQ-like decompositions that derive their methodology from the collage transform and from concepts of fractal geometry [16]. Due to an obscure formulation and high cost of the forward transformation, fractal-based compression remains an experimental technique.
Recently-published research by Chen and Bovik [1] has reconsidered the problem of compression based upon HVS-based knowledge of exemplar patterns that may be used by the visual cortex to partition imagery. For example, the visual cortex is known to contain simple, complex, and hypercomplex cells [17] that mediate receptive fields which detect bar- or wedge-shaped gradients, as well as feature orientation and (possibly) shape. Chen has exploited this information to modify block truncation coding by replacing the costly bitmap construction step with a simple correlation step that finds the best match between the zero crossing configuration and a small set of exemplar blocks. This method, called visual pattern image coding (VPIC), yields high computational efficiency with respect to BTC or VQ and combines advantages of both methods. Given the appropriate set of exemplar patterns, Chen has demonstrated (on several well-known test images such a mandrill and lena) high reconstruction fidelity at compression ratios of 20:1 to 40:1, which appears to be superior to JPEG's performance at such compression levels.
Pyramidal coding has advanced somewhat since its early years, leading to hierarchical compression transforms such as EPIC [18,19] and SPIHT [20,21]. Such transforms boast compression ratios of 100:1 without appreciable image degradations, but tend to concentrate representational error in regions of high variance. Since these areas of detail are usually where interesting objects are found (e.g., targets in military images), EPIC and SPIHT may not be useful for compressing surveillance images. A novel transform, called BLAST (an acronym for Blurring, Local Averaging, Sharpening, and Thresholding) has been developed by Schmalz and Ritter [22] that achieves compression ratios comparable to EPIC and SPIHT but distributes error uniformly throughout the reconstructed (decompressed) image. BLAST has the additional advantage of being data-independent, since the transform parameters vary with the size of the encoding block and computational cost constraints. In practice, BLAST can be implemented with local operations using simple arithmetic functions only, which makes BLAST attractive for SIMD-parallel meshes with small local memories.
To better understand data compression from a mathematical perspective, we next discuss basic concepts of information theory.
1.2. Overview of Information Theory.
Information theory is an important subdiscipline of mathematics that emerged from cryptologic research in the late 1940s. Primarily deriving from the work of Claude Shannon [26] at Bell Laboratories, information theory provides a rigorous framework for modelling the content of messages in cryptology in terms of the number of bits required to encode each symbol.In this section, we present an introduction to information theory that also clarifies related concepts of data compression. For those who are more mathematically inclined, excellent discussions of information theory are given in [23] and [24].
1.2.1. Entropy.
- Observation. Assume that processes P1 and
P2 have n1 and n2 equiprobable
outcomes, respectively. If the outputs of P1 and
P2 are combined to yield the output of a process
P3, then P3 has n3 =
n1 · n2 equiprobable outcomes. The
computation of n3 is described as follows.
Assumption. Let P1,P2,P3 :
F -> F and let
n1 = |range(P1)|
with n2 = |range(P2)|. If P3
is obtained from some function of the output of P1 and
P2, then domain(P3)
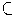 range(P1)
× range(P2). However, we previously assumed
that range(Pi) = domain(Pi) for
i = 1..3. The preceding expression can thus be rewritten as:
range(P1)
× range(P2). However, we previously assumed
that range(Pi) = domain(Pi) for
i = 1..3. The preceding expression can thus be rewritten as:
range(P3)which implies that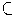 range(P1)
× range(P2),
|range(P3)| < |range(P1)| · |range(P2)| .In the limiting case, where the preceding relation is the equality relation, we have n3 = n1 · n2. Observation. The amount of information output by a continually productive source is a strictly increasing function of time.
range(P1)
× range(P2),
|range(P3)| < |range(P1)| · |range(P2)| .In the limiting case, where the preceding relation is the equality relation, we have n3 = n1 · n2. Observation. The amount of information output by a continually productive source is a strictly increasing function of time.
Definition. Let H denote the information content (or entropy) of a process, and let H denote the operation that computes H. In the first Observation of this section, if Hi = H(Pi) for i = 1..3, then the entropy of P3 is given by H3 = H1 + H2.
- Assumption. Let the number of equiprobable outcomes of
a process P : F -> F be determined by a function
N : (F -> F) -> N, where
domain(N) denotes a process. Assume that a
function f combines two processes of form F -> F
to yield a process of form F -> F. What analytically
tractable function embodies the concept expressed in the
composition N o f?
Lemma 1. Given the preceding assumption and processes
P1,P1 : F -> F, the
entropy H(P3) of a process P3 =
f(P1,P2) is given by
H(P3) = log(n3) = log(N(P3))if the following conditions are satisfied:
- P1 and P2 have equiprobable outcomes n1 = N(P1) and n2 = N(P2).
- P3 has n3 = n1 · n2 equiprobable outcomes.
- If Hi = H(Pi) for i = 1..3, then H3 = H1 + H2.
- Proof. Assume that conditions 1-3 hold.
Note that H = log is the only function that
satisfies conditions 1-3 simultaneously, since
n3 = n1 · n2,
H(P3) = log(n3) =
log(N(P3)), and
log(n3) = log(n1·n2) = log(n1) + log(n2) .Thus, if H = log, then H3 = H1 + H2, and the lemma holds.
We next explore the case when two processes have outcomes that are not equiprobable.
- Remark. Suppose we have two processes P1 and
P2 with n1 and n2 equiprobable
outcomes. Let probabilities p1 and p2
be associated with n1 and n2, such that
n = n1 + n2 and
pi = ni/n , where i = 1,2 .Recall that the entropy associated with one message among n equally likely outcomes is denoted by H(n) = log(n). However, for n1/n of the time, H(n1) = log(n1). Symmetrically, H(n2) = log(n2). Thus, the net entropy is given byH = log(n) - (n1/n)·log(n1) - (n2/n)·log(n2) ,which can be expressed in terms of probabilities as:H = -(p1/n)·log(p1) - (p2/n)·log(p2) .Since p1,p2 < 0, the logarithms are negative and H > 0.
1.2.2. Relationship of Entropy to Probability.
Via the preceding equation, we can express information content in terms of a discrete probability distribution over a random variable. The following theorem is illustrative.- Theorem 2. Let a process P have n possible outcomes that
exhibit individual probabilities pi, where i = 1..n.
The entropy of P, denoted by H(P), is given by
- Theorem 3. If a process P is comprised of two statistically
independent processes P1 and P2, then the
entropy of P is given by
H(P) = H(P1) + H(P2) .Theorem 4. If a process P is comprised of two processes P1 and P2 that are not statistically independent, then the entropy of P is given byH(P) < H(P1) + H(P2) .The following theorem of maximum information is stated without proof, which could be assigned as an exercise or as a homework problem. Theorem 5. If a discrete process P has n outcomes that exhibit individual probabilities pi, i = 1..n, then P yields maximum information when pi = 1/n.
Definition. If an alphabet has n symbols, then the average rate is given by log(n)/n bits per symbol.
Example. The modern English alphabet F has 26 symbols plus the ten digits 0-9. Excluding the digits, H(F) = log(26) = 4.5 bits/symbol. If the probability of each letter is taken into account and we apply Equation (I), then H(F) < 4 bits/symbol. Using a text corpus abstracted from technical documents, Shannon showed that the actual information content of English is approximately one bit per symbol, since the nonuniform distribution of n-grams (groups of n consecutive symbols) implies statistical dependence among symbols. In practice, various entropy values can be obtained using different text corpi expressed in other languages. As this class progresses, we will see that this concept also applies to imagery and databases.
We next discuss the computation of measures of information content in text.
Example. Assume that the substitution cipher T : FX × K -> FX, where K is called the keyspace and T is one-to-one and onto. Let |F| = 26, as before, and let K = F. Recall from previous examples that there are 26! (i.e., |F|!) possible keys of length 26 symbols.
Let us construct a 26-character key that encrypts a 40-character text (i.e., |X| = 40). The information content of the key is given by Hk = log(|F|!) = log(26!). If the plaintext has entropy
Ht, then the substitution has entropy H(T) < Ht + Hk, since the plaintext and key may not be statistically independent.
From Theorem 5, a 40-character text has maximum entropy
Substituting the maximum entropy for Ht, we obtain: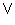 (H(T))
(H(T))
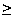 Ht + Hk = Ht +
log(26!) .
HtAt 100 bits per 40 characters, we have an average rate of 2.5 bits per symbol, which is considerably less than the maximum information content of text (4 bits per symbol) computed in the preceding example.
Ht + Hk = Ht +
log(26!) .
HtAt 100 bits per 40 characters, we have an average rate of 2.5 bits per symbol, which is considerably less than the maximum information content of text (4 bits per symbol) computed in the preceding example.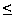
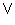 (Ht)
- Hk = 40 · log(26) - log(26)!
= 100 bits .
(Ht)
- Hk = 40 · log(26) - log(26)!
= 100 bits .
H(P) = 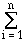 -pi · logpi .
-pi · logpi .

 (I)
(I)
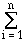 -pi · logpi .
-pi · logpi .

 (I)
(I)
- Proof. The proof, which is well known, follows
from the preceding remark and
induction on i.

1.2.3. Entropy and Data Compression.
We began this section by stating that a constant-valued image could be represented by one value. Since this value can be stored offline and can be indexed by one bit, a constant-valued image that has n pixels would be compressed to yield a minimum possible entropy of 1/n bits per pixel (bpp). Similarly, a uniformly random image would not be compressible. That is, if the random source image has entropy of m bpp, then the compressed image would have maximum entropy of m bpp. These bounds illustrate the limits of data compression, whose primary purpose is entropy reduction. In the following discussion, we shall see that data compression can facilitate transmission of high-entropy data across low-bandwidth channels by first compressing the data.- Observation. If a channel has bandwidth B bits/second (bps)
and one wishes to transmit D > B bits of data per second along
this channel, then a compression ratio, given by
CRis required to transmit the data. Example. Suppose we have an image a that is represented by 8 bpp and a compression transform T that can be applied to a. If T has CR = 10:1, then the entropy of the compressed image
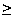 D/B ,
D/B ,
ac = T(a)is computed asH(ac) = H(a) / CR = 8bpp / 10 = 0.8 bpp .Remark. The compression ratios that are attainable without significant information loss depend upon several factors, namely,
- Noise levels in the source imagery, where noise is assumed to consist of random fluctuations, and hence is mathematically irreducible (i.e., uncompressible);
- Statistics of the signal (i.e., non-noise) portion of the image, which can bias statistically-based transforms toward compression ratios that differ significantly from those predicted by theory; and
- Spatial content of the signal, which tends to bias the compression ratio of a transform that is based upon encoding of image feature shape and size.
1.3. Overview of Human Visual System and Image Compression
The human visual system (HVS) is comprised of several complex organs, not the least of which is the brain itself. In order of light reception and transmission, one encounters the- Globe and orbit (i.e., eyeball and socket)
- Retina (photoreceptors at the back of the eyeball)
- Optic nerve and chiasm (like a telephone cable and splitter)
- Optic tracts and radiations (similar to a local-area network)
- Visual cortex (where vision actually occurs)
We discuss each of these structures and processing centers, as follows.
1.3.1. Globe and Orbit.
The eyeball or globe contains the transmission window (cornea), focusing mechanism (lens and ciliary body), with a fluid (aqueous humor) and a jelly (vitreous humor) that fill the globe, thereby giving it necessary structural rigidity. The globe is rotated in the orbit (the eye socket) by six muscles which are directly controlled by cranial nerves. The orbit is filled with fat that cushions the globe and its fragile internal structures, and is well-supplied with lubricants such as tears, various mucoid secretions, and oily secretions from the Meibomian glands on the eyelids. The Meibomian glands can become clogged, thus forming a painful hordeolum (sty) or chalazion (granulomatous sty), which many humans experience at one time or another. The exterior of the globe is covered in a glassy mucous membrane called the conjunctiva, which can become inflamed when exposed to viruses or bacteria. For example, many Florida residents experience swimming-pool conjunctivitis, so-called because it is often contracted in public swimming pools. The eye's internal pressure, which is maintained by aqueous humor secretion and drainage processes, is called intra-ocular pressure (IOP) and, when excessive (usually > 15mm Hg in the adult) is responsible for the onset of glaucoma. At its worst, glaucoma exerts dangerously high pressure on the vessels and associated structures of the retina (the matrix of photoreceptors at the back or posterior portion of the globe). This effect can cause ischemia (oxygen deprivation) in the retina, due to constriction of the blood vessels, which can lead to visual field loss.IOP is controlled by a sophisticated and incompletely understood chemical mechanism that is dependent upon one's age, gender, health, state of rest, posture, altitude above sea level, state of arousal, etc. Glaucoma can be medicated using eyedrops that contain chemicals which inhibit aqueous humor secretion and/or open the drainage ducts in the anterior chamber, which is between the cornea and the lens. Extreme cases of glaucoma may require surgery to enlarge the drainage channels, thereby reducing IOP.
Since there are extensively many eye disorders, only two of which (i.e., field distortion and color blindness) are mentioned in this class, we hereafter assume (unless otherwise stated) that the HVS is a normal, healthy system.
References.
[1] Chen, D. and A.C. Bovik. "Visual pattern image coding", IEEE Transactions on Communications 38:2137-2146 (1990). [2] Duff, I.S., R.G. Grimes, and J.G. Lewis. "Sparse matrix test problems", ACM Transactions on Mathematical Software 15:1-14 (1989).[3] Liu, J.W.H. "The multifrontal method for sparse matrix solution: theory and practice", SIAM Review 34:82-109 (1992).
[4] Oehler, K.L., P.C. Cosman, R.M. Gray, and J. May. "Classification using vector quantization", Proceedings of the 25th Annual Asilomar Conference on Signals, Systems, and Computers (Pacific Grove, CA, Nov. 1991), pp. 439-445 (1991).
[5] Netravali, A.N. and J.O Limb. "Picture coding: A review", Proceedings of the IEEE 68:366-406 (1980).
[6] Zschunke, W. "DPCM picture coding with adaptive prediction", IEEE Transactions on Communication COM-25(11):1295-1302 (1977).
[7] Li, W. and Y.Q. Zhang. "Vector-based signal processing and quantization for image and video compression", Proceedings of the IEEE 83:317-335 (1995).
[8] Healy, D.J. and O.R. Mitchell. "Digital video bandwidth compression using block truncation encoding", IEEE Transactions on Communication COM-29(12):1809-1817 (1981).
[9] Kunt, M. M. Bernard, and R. Leonardi. "Recent results in high-compression image coding", IEEE Transactions on Circuits and Systems CAS-34(11):1306-36 (1987).
[10] Baron, S. and W.R. Wilson. "MPEG overview", SMPTE Journal 103:391-394 (1994).
[11] Felician, L. and A. Gentili. "A nearly-optimal Huffman encoding technique in the microcomputer environment", Information Systems (UK) 12(4):371-373 (1987).
[12] Shoaff, W.D. "The Singular Value Decomposition Implemented in Image Algebra", M.S. Thesis, Department of Computer and Information Sciences, University of Florida (1986).
[13] Ohta, Mutsumi, and S. Nogaki. "Hybrid picture coding with wavelet transform and overlapped motion-compensated interframe prediction coding", IEEE Transactions on Signal Processing 41:3416-3424 (1993).
[14] Dettmer, R. "Form and function: Fractal-based image compression", IEE Review 38:323-327 (1992).
[15] Bani-Eqbal, B. "Enhancing the speed of fractal image compression", Optical Engineering 34:1705-1710 (1995).
[16] Mandelbrot, B.B. The Fractal Geometry of Nature, 2nd Edition, New York: W.H. Freeman (1983).
[17] Barlow, H.B., and P. Fatt, Eds. Vertebrate Photoreception, New York: Academic Press ((1976).
[18] Adelson, E.H. and E.P. Simoncelli. "Subband image coding with three-tap pyramids", in Proceedings of the 1990 Picture Coding Symposium (1990).
[19] Simoncelli, E.P. and E.H. Adelson. "Non-separable extensions of quadrature mirror filters to multiple dimensions", in Proceedings of the IEEE: Special Issue on Multidimensional Signal Processing (April 1990).
[20] Said, A. and W. A. Pearlman. "A New Fast and Efficient Image Codec Based on Set Partitioning in Hierarchical Trees", IEEE Transactions on Circuits and Systems for Video Technology 6:243-250 (1996).
[21] Said, A. and W. A. Pearlman. "An Image Multiresolution Representation for Lossless and Lossy Image Compression", IEEE Transactions on Image Processing 5:1303-1310 (1996).
[22] Schmalz, M.S., G.X. Ritter, and F.M. Caimi. "Performance analysis of compression algorithms for noisy multispectral underwater imagery of small targets", in Proceedings SPIE 3079 (1997).
[23] Hamming, R.W. Coding and Information Theory, Englewood Cliffs, NJ: Prentice-Hall (1986).
[24] McEliece, R. The Theory of Information and Coding: A Mathematical Framework for Communication, Reading, MA: Addison-Wesley (1977).
[25] Patterson, W. Mathematical Cryptology for Computer Scientists and Mathematicians, Totowa, NJ:Rowan and Littlefield (1987).
[26] Shannon, C. Mathematical Theory of Communication, Urbana, IL: University of Illinois Press (1949).
No comments:
Post a Comment