31.1 Definitions for Rooted Trees
The figure shows a rooted tree with edges undirected from child to parent. The nodes are labelled for convenience. The tree has degree 3 since the node with maximum degree (the root, node A) has degree 3. The more traditional way to draw the tree is with undirected edges; this is also shown in the figure.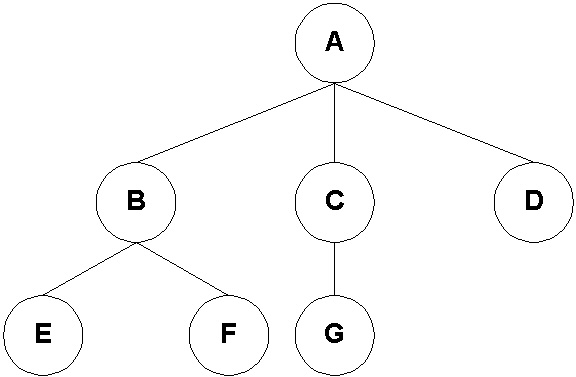
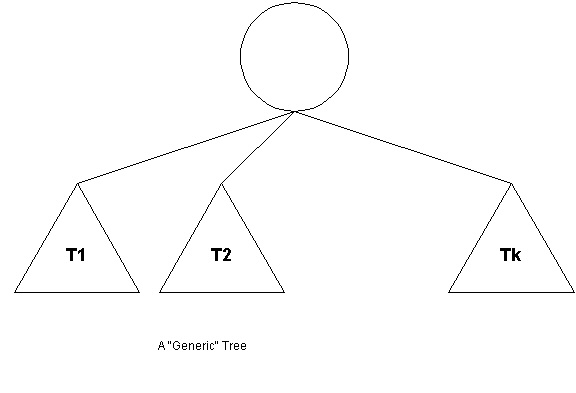
Generic trees are usually shown in a schematic form with the subtrees indicated by triangles. The firgure below shows such a representation. The details of the subtrees are hidden in the "triangles'"
Theorem There are n - 1 edges in any tree with n nodes Proof: Each edge connects a node to its parent. Every node except the root has a parent.
struct general_node
{
Element_Type element;
general_node * child1;
general_node * child2;
general_node * child3;
general_node * child4;
.
.
.
};
An obvious problem with this representation is that the number of
children would have to be large enough to cover all the expected cases.
This would usually mean wasting a lot of pointers.
A better representation is the ``firstchild, nextsibling'' representation.
struct general_node
{
Element_Type element;
general_node *first_child;
general_node *next_sibling;
};
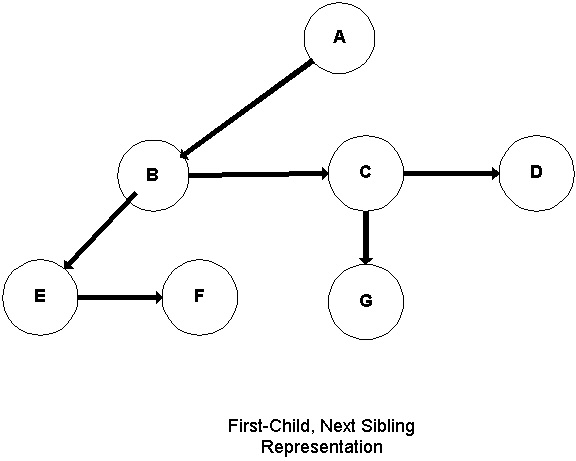
The figure below shows the "firstchild, nextsibling" representation of the
rooted tree shown above.. The downwardpointing edges are the "first-child" edges. The
horizontal edges are the "next-sibling" edges.
Here's the definition of a Tree Node for binary trees. It keeps pointers
to its left and right children.
// forward declaration
template <class Etype> class Binary_Search_Tree;
template <class Etype>
class Tree_Node
{
protected:
Etype Element;
Tree_Node *Left;
Tree_Node *Right;
Tree_Node( Etype E = 0, Tree_Node *L = NULL, Tree_Node *R = NULL )
: Element( E ), Left( L ), Right( R ) { }
friend class Binary_Search_Tree<Etype>;
};
Binary Search Tree is made a friend of Tree Node.
The constructor takes an element and two pointers as arguments (with
default values for all). The constructor can be called in any of the following ways:
1. Tree_Node();
in this case Element will be 0, and both Left and Right children will
be NULL.
2. Tree_Node(elementvalue);
in this case, Element will have the value elementvalue, Left and
Right will be NULL.
3. Tree_Node(elementvalue, nodeptr1);
in this case, Element will have the value elementvalue, Left will
have the value nodeptr1 and Right will be NULL. < BR>
4. Tree_Node(elementvalue, nodeptr1, nodeptr2);
in this case, Element will have the value elementvalue, Left will
have the value nodeptr1 and Right will have the value nodeptr2.
Theorem 32.1 If a binary tree (BT) of height h has t leaves, then h >= lg t
Proof: If h >= lg t, then equivalently t <= 2 h . We prove the latter by induction on h.
Base: h = 0 (single node). Therefore, t = 1 = 20
IH: Assume true for every BT with height less than h
Let T be a BT of height h > 0 and with t leaf nodes. We consider two
possible cases:
Case 1: Root of T has only one child. Without loss of generality, let it be
the left child. Then the left subtree has height h - 1 and it has all
the leaf nodes of T. By IH, t <= 2 h - 1 < 2h
Case 2: Root has two children. Let t1 and t2 be the number of leaf nodes and h 1 and h 2 the heights
of the two subtrees, respectively. Since the leaf nodes of T are partitioned between the two subtrees,
t = t1 + t2.
By IH, t1 <= 2h1 and t 2 <= 2 h 2 . Also, h1 <= h - 1 and h 2 <= h - 1
Therefore,
t <= 2h1 + 2h2
t <= 2h - 1 + 2h - 1
t <= 2h
Theorem 32.2 A full binary tree (FBT) of height h has 2h leaf nodes.
Proof: By induction on h
Base: A FBT of height 0 has 1 node (the root).
IH: Assume all full binary trees of height h, 0 < h <= H have 2 h leaf nodes.
For a FBT, T, of height H, create a new FBT T' by adding exactly two
children to each leaf of T . The height of T' is H + 1 and T' has twice the
nuber of leaf nodes as T , namely 2 X 2H = 2 H+1.
Theorem 32.3 The number of nodes in a full binary tree of height h is 2 h+1 - 1
Proof: The number of nodes is the sum of the number of nodes on each
level, l. Since there are 2l nodes at each level, the total number of nodes is
SUMht=0 2t
= 2h+1 - 1
The equation is easily proven by induction.
Theorem 32.4 If n is the number of nodes in a complete binary tree (CBT)
of height h, then 2h <= n < 2h+1
Proof: A CBT of height h has at least one and as many as 2h nodes at
level h (the final level is not empty, and may be full). In any event, level
h - 1, (h > 0) ,must be full by definition of a CBT. The number of nodes in a
FBT of height h - 1 is 2(h - 1) + 1 - 1. (By Theorem 32.3 above)
A CBT of height h has at least one more node than a FBT of height h - 1.
Therefore, the number of nodes n in a CBT is bounded by
2(h - 1) + 1 - 1 + 1 <= n <= 2h+1 - 1
Therefore,
2h <= n < 2h+1
Equivalently, we can say h <= lg n < h + 1.
- DEFINITION: A tree is a set of nodes, perhaps empty. If not empty,
there is a distinguished node r, called root and zero or more subtrees
T1,T2,.....Tk each of whose roots are connected by a directed edge to r.
The root of each subtree is called a child of r, and r is called the parent of each child.
- DEFINITION: Nodes with no children are called leaf nodes. All other
nodes are called interior nodes.
- DEFINITION: The degree of a node is the number of its children.
The degree of a tree is the maximum degree of any of its nodes.
- DEFINITION: Nodes with the same parent are called siblings.
- There is such a thing as a NULL tree -- a tree with no nodes. Not every
author allows this.
- Trees defined this way are "rooted'' trees. They have a distinguished root.
Not all trees are considered to be rooted.
- Nodes are sometimes called vertices or points; edges are sometimes called lines.
- Note that the edges are directed edges. This means there is a direction
associated with them. This definition has the edges directed to the root.
Nobody draws the edges as directed edges, it's just understood.
The figure shows a rooted tree with edges undirected from child to parent. The nodes are labelled for convenience. The tree has degree 3 since the node with maximum degree (the root, node A) has degree 3. The more traditional way to draw the tree is with undirected edges; this is also shown in the figure.

Generic trees are usually shown in a schematic form with the subtrees indicated by triangles. The firgure below shows such a representation. The details of the subtrees are hidden in the "triangles'"

- DEFINITION: A path from node n1 to node nk is a sequence of nodes
n1, n2,....., nk such that ni is the parent of n i+1 for 1 <= i < k.
The length of this path is the number of edges on the path (namely k - 1)
- There is a path of length zero from every node to itself.
- In a tree there is one and only one path from the root to each node.
- DEFINITION: The depth of a node is the length of the path from
the root to the node
- The root is at depth 0.
- DEFINITION: The depth of a tree is the depth of its deepest leaf.
- DEFINITION: The height of any node is the longest path from the
node to any leaf.
- The height of any leaf is 0.
- DEFINITION: The height of a tree is the height of its root.
- The height and depth of a tree are equal.
- DEFINITION: If there is a path from node ni to node nj, then node
ni is an ancestor of node nj and
node nj is a descendent of node ni.
- Every node is both an ancestor and a descendent of itself. An ancestor
(descendent) of a node which is not the node itself is called a proper
ancestor (descendent) of the node.
31.2 Theorems about Trees
Theorem There are n - 1 edges in any tree with n nodes Proof: Each edge connects a node to its parent. Every node except the root has a parent.
31.3 FirstChild, NextSibling Representation of General Rooted Trees
One could imagine representing a general node as a struct:struct general_node
{
Element_Type element;
general_node * child1;
general_node * child2;
general_node * child3;
general_node * child4;
.
.
.
};
An obvious problem with this representation is that the number of
children would have to be large enough to cover all the expected cases.
This would usually mean wasting a lot of pointers.
A better representation is the ``firstchild, nextsibling'' representation.
struct general_node
{
Element_Type element;
general_node *first_child;
general_node *next_sibling;
};
The figure below shows the "firstchild, nextsibling" representation of the
rooted tree shown above.. The downwardpointing edges are the "first-child" edges. The
horizontal edges are the "next-sibling" edges.

32 Binary Trees
- DEFINITION: A binary tree is a rooted tree in which no node can
have more than two children, and the children are distinguished as left and right.
- Not every rooted tree with degree two is a binary tree. The children must
be in order -- there is a "left'' child and a "right'' child.
- DEFINITION: A full binary tree is one in which every leaf node is at
the same level, and every interior node has exactly two children.
- DEFINITION: A complete binary tree is a full binary tree except
perhaps for the final level which is filled from left to right.
Here's the definition of a Tree Node for binary trees. It keeps pointers
to its left and right children.
// forward declaration
template <class Etype> class Binary_Search_Tree;
template <class Etype>
class Tree_Node
{
protected:
Etype Element;
Tree_Node *Left;
Tree_Node *Right;
Tree_Node( Etype E = 0, Tree_Node *L = NULL, Tree_Node *R = NULL )
: Element( E ), Left( L ), Right( R ) { }
friend class Binary_Search_Tree<Etype>;
};
Binary Search Tree is made a friend of Tree Node.
The constructor takes an element and two pointers as arguments (with
default values for all). The constructor can be called in any of the following ways:
1. Tree_Node();
in this case Element will be 0, and both Left and Right children will
be NULL.
2. Tree_Node(elementvalue);
in this case, Element will have the value elementvalue, Left and
Right will be NULL.
3. Tree_Node(elementvalue, nodeptr1);
in this case, Element will have the value elementvalue, Left will
have the value nodeptr1 and Right will be NULL. < BR>
4. Tree_Node(elementvalue, nodeptr1, nodeptr2);
in this case, Element will have the value elementvalue, Left will
have the value nodeptr1 and Right will have the value nodeptr2.
32.1 Theorems About Binary Trees
Theorem 32.1 If a binary tree (BT) of height h has t leaves, then h >= lg t
Proof: If h >= lg t, then equivalently t <= 2 h . We prove the latter by induction on h.
Base: h = 0 (single node). Therefore, t = 1 = 20
IH: Assume true for every BT with height less than h
Let T be a BT of height h > 0 and with t leaf nodes. We consider two
possible cases:
Case 1: Root of T has only one child. Without loss of generality, let it be
the left child. Then the left subtree has height h - 1 and it has all
the leaf nodes of T. By IH, t <= 2 h - 1 < 2h
Case 2: Root has two children. Let t1 and t2 be the number of leaf nodes and h 1 and h 2 the heights
of the two subtrees, respectively. Since the leaf nodes of T are partitioned between the two subtrees,
t = t1 + t2.
By IH, t1 <= 2h1 and t 2 <= 2 h 2 . Also, h1 <= h - 1 and h 2 <= h - 1
Therefore,
t <= 2h1 + 2h2
t <= 2h - 1 + 2h - 1
t <= 2h
Theorem 32.2 A full binary tree (FBT) of height h has 2h leaf nodes.
Proof: By induction on h
Base: A FBT of height 0 has 1 node (the root).
IH: Assume all full binary trees of height h, 0 < h <= H have 2 h leaf nodes.
For a FBT, T, of height H, create a new FBT T' by adding exactly two
children to each leaf of T . The height of T' is H + 1 and T' has twice the
nuber of leaf nodes as T , namely 2 X 2H = 2 H+1.
Theorem 32.3 The number of nodes in a full binary tree of height h is 2 h+1 - 1
Proof: The number of nodes is the sum of the number of nodes on each
level, l. Since there are 2l nodes at each level, the total number of nodes is
Theorem 32.4 If n is the number of nodes in a complete binary tree (CBT)
of height h, then 2h <= n < 2h+1
Proof: A CBT of height h has at least one and as many as 2h nodes at
level h (the final level is not empty, and may be full). In any event, level
h - 1, (h > 0) ,must be full by definition of a CBT. The number of nodes in a
FBT of height h - 1 is 2(h - 1) + 1 - 1. (By Theorem 32.3 above)
A CBT of height h has at least one more node than a FBT of height h - 1.
Therefore, the number of nodes n in a CBT is bounded by
No comments:
Post a Comment