AVL Trees

36.1 Height­Balanced Binary Trees 
Most operations on binary trees have asymptotic performance given by O(h), where h is the height of the tree. In compact binary trees, tree height 
is approximately equal to lg n, where n is the number of nodes in the tree. It is therefore desirable to build trees which are reasonably compact. One 
way to do this is to require that the tree be height balanced. 

DEFINITION: An empty binary tree is height balanced. If T is a non­empty binary tree with TL and TR as left and right subtrees, 
respectively, then T is height balanced if and only if 
    1. TL and TR are height balanced, and 
    2. |hR - hL| <= 1 where hR and hL are the heights of TR and TL respectively

A less formal. but equivalent definition of height balance is

DEFINITION: A height-balanced binary tree is one for which at every node, the absolute value of the difference in heights of the left and right 
children is no larger than one. 

Note: Every complete binary tree is height­balanced. 

Theorem 36.1 The largest number of nodes in a height­balanced binary tree (HBT) of height h is 2 h+1 
Proof: The most compact HBT is a FBT and this is the number of nodes in an FBT.

DEFINITION: An AVL Tree is a height-balanced binary search tree.

DEFINITION: The balance factor of a binary tree is the difference in heights of its two subtrees (hR - hL).  The balance factor (bf) of a height
balanced binary tree may take on one of the values -1, 0, +1.

An AVL node is "left­heavy" when bf = ­1, "equal­height" when bf = 0, and "right­heavy" when bf = +1 




36.2 Rebalancing an AVL Tree 
Theorem 36.2 An AVL tree whose root has zero balance factor cannot be unbalanced by the insertion of a single node.

Proof: A new node will be added as a leaf to one of the subtrees, increasing that subtree's height by (at most) 1. Therefore, the balance 
factor of the tree may change to +1 or -1, keeping the tree balanced.

An AVL tree with non-zero balance factor may become unbalanced (balance factor becomes +2 or -2) upon insertion of a new node.



An AVL tree which becomes unbalanced by insertion of a node can be re­balanced by performing one or more rotations. 



Rotate_Right means rotate from the right toward the left. The right child is rotated about the node. The other way for Rotate_Left.



36.2.1 Rotations Are Dictated by a Node's Children 
When rebalancing is to be done at a node, the type of rotations depends on the balance factor at the right or left child. There are two rebalancing cases 
for right child and two cases for left child. Here are the two right child cases (the left child cases are symmetric). 

Case 1: Right Child's Balance Factor Becomes +1 

Figure 36.1 shows an abstract AVL tree for case 1. In this case, the balance factor of the right subtree of R becomes +1 because Z is 
added to XR . The tree rooted at R (which may itself be a subtree) has balance factor +1 before node Z is inserted and +2 afterwards. 
To rebalance the tree, a Rotate_Right is performed at R. The resulting abstract AVL tree is shown. Note that the height of the tree 
after re­balancing is the same as the height before insertion of the new node.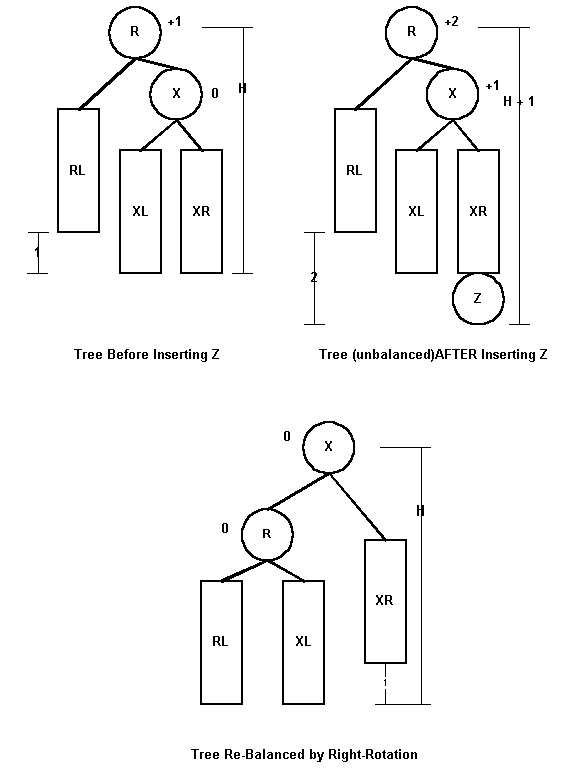 






Figure 36.1: Insertion in AVL Tree (Case 1)




Case 2: Right Child's Balance Factor Becomes -1

Figure 36.2 shows an abstract AVL tree for case 2.  In this case,the balance factor of the right subtree of R becomes -1 because Z
is added to XL.  As in case 1, the balance factor of R changes from+1 to +2.  To rebalance the tree, two rotations will be necessary.
The first rotation will be rotate­left around X; the second rotation will be rotate­right around R. The figure shows XL expanded to show its 
root W and subtrees. There are two possibilities for W . Since it doesn't matter in the final analysis, we pursue only one of the two 
possibilities. Figure 36.3 shows the re­balanced tree after left­rotation about X and right­rotation about R. 

Note that the height of the tree after re­balancing is the same as the height before insertion of the new node. 


 


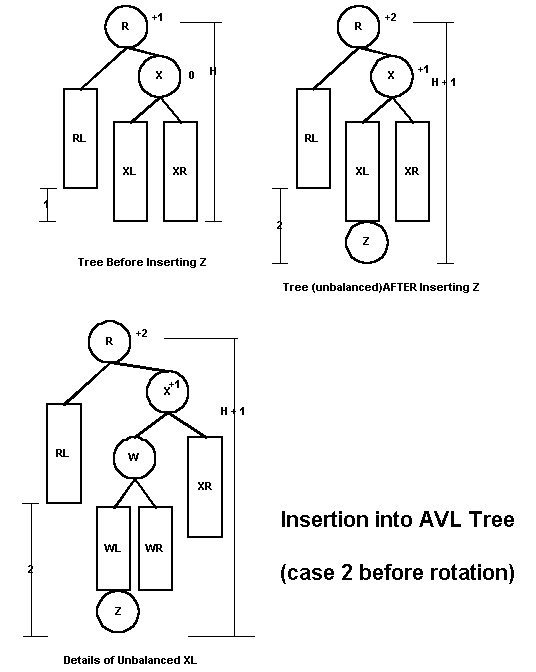
Figure 36.3: Insertion in AVL Tree (Case 2 after rotations) 




36.3 Implementation of AVL Tree 


template <class Etype>
class Avl_Node : public Tree_Node<Etype>
{
  private: 
    int Height; 
    friend int Node_Ht( Avl_Node *P ) 
      { return P ? P­>Height : ­1; }
    friend int Node_Ht( Tree_Node<Etype> *P ) 
      { return Node_Ht( ( Avl_Node<Etype> * ) P ); }
    friend void Calculate_Height( Avl_Node *P ) 
      { P­>Height = 1 + Max( Node_Ht( P­>Left ), Node_Ht( P­>Right ) ); }
    friend void S_Rotate_Left( Avl_Node * & k2 ); 
    friend void D_Rotate_Left( Avl_Node * & k3 ); 
    friend void S_Rotate_Right( Avl_Node * & k1 ); 
    friend void D_Rotate_Right( Avl_Node * & k3 ); 

  protected: 
    friend class Avl_Tree<Etype>; 

  public: 
    Avl_Node( Etype E = 0, Avl_Node *L = NULL, Avl_Node *R = NULL, int H = 0 )
      : Tree-Node<Etype>( E, L, R ), Height( H ) { }
}; 

Note that the height of a NULL node is defined as ­1 in Node_Ht. 

Node_Ht is overloaded to avoid having to make type conversions from Tree_Node to Avl_Node on every call. 

Note that the constructor for Avl_Node calls the constructor for Tree_Node in the initialization. 

Avl_Node is derived from Tree_Node. It inherits the Element, Left, and Right fields. 

The Avl Node maintains a data member Height, but does not maintain a balance factor. 
When it needs the balance factor, it computes the height of the nodes left and right subtrees (i.e., it computes the balance factor). 

template <class Etype>
class Avl_Tree : public Binary_Search_Tree<Etype>
{ 
  protected: 
    Avl_Node<Etype> * Copy( const Avl_Node<Etype> *T ); 
    void Insert( const Etype & X, Avl_Node<Etype> * & T ); 
    void Remove( const Etype & X, Avl_Node<Etype> * & T ); 

  public: 
    Avl_Tree( ) : Binary_Search_Tree<Etype>( ) { } 
    const Avl_Tree & operator = ( const Avl_Tree & Value ); 
    virtual void Insert( const Etype & X ) 
      { Insert( X, (Avl_Node<Etype> * & ) Root ); }
    virtual void Remove( const Etype & X ) 
      { Remove( X, ( Avl_Node<Etype> * & ) Root ); }
}; 

Avl_Tree is derived from Binary_Search_Tree. It overrides the member functions Insert and Remove. 
Insert and Remove are overloaded. The public functions call the protected functions. 





36.4 Inserting a Node in an AVL Tree 


The Insert procedure for AVL trees does a node insertion just like node insertion in a binary search tree (BST). Each recursive call takes you 
further down the tree until the insertion point is found. 

In BST, we are satisfied to simply go back up the recursion without doing any more work. In AVL, we do some work at each node on the way back up;
namely we adjust the balance factors and perhaps do a rebalance. 

template <class Etype>
void Avl_Tree<Etype>:: 
Insert( const Etype & X, Avl_Node<Etype> * & T ) 
{
  if( T == NULL ) // Create a one node tree. 
  { 
    T = new Avl_Node<Etype>( X ); 
    if( T == NULL ) 
      Error( ''Out of space'' ); 
    return; 
  } 

  if( X < T­>Element ) 
  { 
    Insert( X, ( Avl_Node<Etype> * & ) T­>Left ); 
    if( Node_Ht( T­>Left ) ­ Node_Ht( T­>Right ) == 2 ) 
      if( X < ( ( Avl_Node<Etype> * ) T­>Left )­>Element ) 
        S_Rotate_Left( T ); // X is left descendent of T (case 1) 
      else 
        D_Rotate_Left( T ); // X is right descendent of T (case 2) 
    else 
      Calculate_Height( T ); 
  } 
  else if( X > T­>Element ) 
  { 
    Insert( X, ( Avl_Node<Etype> * & ) T­>Right ); 
    if( Node_Ht( T­>Right ) ­ Node_Ht( T­>Left ) == 2 ) 
    if( X > ( ( Avl_Node<Etype> * ) T­>Right )­>Element ) 
      S_Rotate_Right( T ); // X is right descendent of T (case 1) 
    else 
      D_Rotate_Right( T ); // X is left descendent of T (case 2) 
    else 
      Calculate_Height( T ); 
  }
  // Else x is in the tree already, so we'll do nothing. 
}

QUESTION: How costly is the computation of the balance factor each time? 

ANSWER: 



QUESTION: How costly would the computation be if balance factor data were stored at each node? 

ANSWER: 
Keeping balance factor data at each node can substantially improve the performance of AVL tree operations. 

EXAMPLE: If newnode was attached to the left branch of the node, the balance factor of the node will change. Think of it as a balance arm. If it 
was balanced (bf = 0), it now tilts down on the left (bf = ­1). If it was tilted to the right (bf = +1), it now becomes balanced (bf = 0). However, if 
it was already tilted to the left (bf = ­1), it becomes over­tilted to the left and we must rebalance (LeftBalance) it. Similar (symmetric) changes are 
made to the node if the newnode is attached to its right branch. 

The following table summarizes the balance factor changes: 

new node         old BF      new BF 
attached           ­1           0 
to                  0          +1 
right              +1          +2 

attached           ­1          ­2 
to                  0          ­1 
left               +1           0 




36.5 Important notes on AVL tree insertions 

  1. Before we start the insertion, the tree is an AVL tree. That means that some nodes may have non­zero balance factors, but no node has 
a balance factor greater than 1 in absolute value. 

  2. We have shown (Figures 36.1, 36.2, and 36.3) that the height of the subtree into which the insertion is made is the same after re­balancing 
as it was before the insertion. This means that we only need to rebalance that subtree, not the entire AVL tree of which it is a part. 

  3. We find the root of the subtree needing rebalancing as we work our way back up the recursion. It is the closest node to the insertion 
point which gets a balance factor of +2 or -1.

36.5.1 Summary of Balance Rules 
The following rules apply when a tree becomes unbalanced after insertion of a new node (the tree balance factor becomes +2 or -2). The rules when the tree 
becomes unbalanced to the left are symmetric to those for the tree becoming unbalanced to the right. 

  1. when the subtree root becomes unbalanced to the right
after insertion of a new node. 
    if root.right is +1 then
      Rotate_Right about root 
    if root.right is ­1 then 
      Rotate_Left about root.right 
      Rotate_Right about root 

  2. when the subtree root becomes unbalanced to the left
after insertion of a new node. 
    if root.left is ­1 then
      Rotate_Left about root 
    if root.left is +1 then 
      Rotate_Right about root.left 
      Rotate_Left about root 

36.5.2 Summary of Balance Factor Changes 
The rules for the new balance factors after re­balancing a tree are also symmetric for right and left unbalance. The following rules are for a tree 
which has become unbalanced to the right (balance factor becomes +2): 

  if root.right is +1 then 
    balance factor of root = 0 
    balance factor of root.right = 0 

  if root.right is ­1 then 
    if balance factor of root.right is 
      0: balance factor of root = 0 
         balance factor of root.right = 0 
         balance factor of root.right.left = 0 

     ­1: balance factor of root = 0 
         balance factor of root.right = +1 
         balance factor of root.right.left = 0 

     +1: balance factor of root = ­1 
         balance factor of root.right = 0 
         balance factor of root.right.left = 0 (new root) 


36.6 Example of Insertions into AVL Tree 


Figure 36.4 shows the growth of an AVL tree in which the values {1, 2, 3, 4, 5, 0, 7, 6} are inserted. The number next to each node
is the balance factor of the node. At each insertion, the tree is shown after the insertion. When re­balancing is done, the rebalanced tree is
also shown. Here's what happens: 

I Insert(1): The node is inserted into an empty AVL tree. The tree remains an AVL tree. 

II Insert(2): The tree remains AVL. 

III Insert(3): Node 1's balance factor is (+2), and its right child's balance factor is +1. This is "case 1", so Rotate_Right about the 
unbalanced node (node 1). 

IV Insert(4): The tree remains AVL. 

V Insert(5): Node 3's balance factor becomes +1, and its right child's balance factor is +1. This is "case 1", so Rotate_Right about the 
unbalanced node (node 3).

VI Insert(0): The tree remains AVL. 

VII Insert(7): The tree remains AVL. 

VIII Insert(6): Node 5's balance factor is +2 and its right child's balance factor is ­1. This is "case 2". Therefore, Rotate_Left about the child 
(node 7) and then Rotate_Right about the unbalanced node (node 5). 

















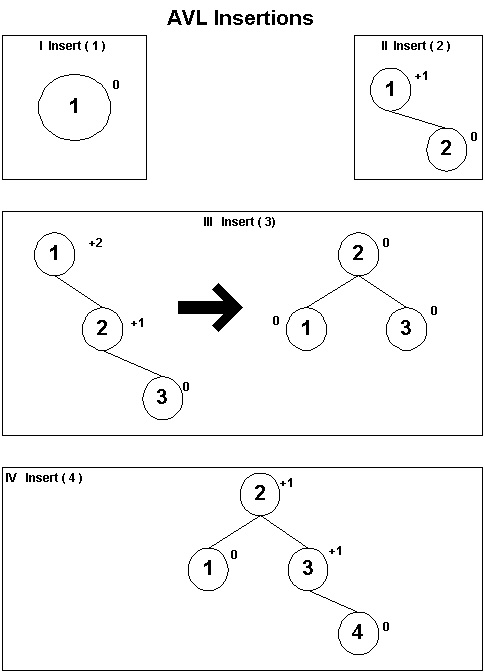
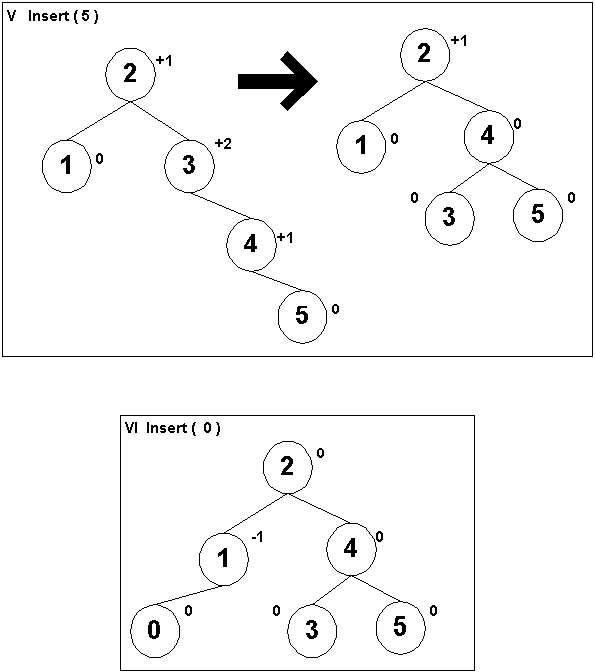
Figure 36.4: Example of Insertion of f1, 2, 3, 4, 5, 0, 7, 6g into an AVL Tree)