Glossary
Countable set : A set is countable if it is finite or has same cardinality as set of natural numbers.
If E F G are three events then
1) only E occurs
means F and G donot occur so EF'G'
2)both E and G but not F
EGF'
3) none of the event occurs
E'F'G'
4)at least one of the event occurs
(E'F'G')' => E U F U G
5)at least two events occurs
EF U EG U FG U EFG
6)all occurs
EFG
7) at most one of them occurs
exactly one of them occurs or none occurs
EF'G' U E'FG' U E'F'G U E'F'G'
8) at most 2 of them occurs
none occurs U exactly one occurs U exactly two occurs
Observations
1) none event occurs(E'F'G') is not complement of all event occurs (EFG)
P(A) probability of event A independent of any other event
P(A U B) = P(A) + P(B) - P(AB)
P(E U F U G) =P(E) + P(F) + P(G) - P(EF) - P(FG) - P(GE) + P(EFG)
P(at least 1 event) = 1- P(neither of 3 events occurs)
Conditional Probability
P(B/A) = P(AB)/P(A)
P(ABC) = P(A/BC)P(BC)
= P(A/BC) P(B/C) P(C)
since we can write
P(AB) = P(B/A) P(A) or
P(AB) = P(A/B) P(B)
Some Counting problems
Problem Find number of ways in which digit 1 appears before digit 4 in permutations of number 12345
number of permutations = permutations in which 1 appears before 4 + permutations in which 1 appears after 4 i.e 2(n) = 5!
n=5!/2
Problem In how many of permutations of number 12345 is first digit greater than second digit
3)second digit 3 first place can be occupied by 1 2
2 * 3!
4) second digit 4
3*4!
5) second digit 5
4*3!
total permutaions in which first digit is less than second = 3!(1+2+3+4) = 10*3!
total permutations in which first digit is greater than second = 5!-10!*3! = 5!/2
1/2(5!)
Solution 2
Since for every permutation abcd (a > b)
there will be also be permutation bacd so all cases are equally likely that 1/2 of these will have first digit greater than second
Problem Suppose we randomly select a permutation from 20! permutations of 1,2,3,4, .....20. what is probability that 2 appears at earlier position than any other even number
Solution 1
for any permutation of number say of digits 1,2,3
123
132
213
231
321
312
Probability of any digit appearing a particular position is equally likely
In above case at position 1, one, two and three all appears twice at position 2 also they appear equal number of time at other positions.
At positon 1 either one can appear or two or three so
P(1)+P(2)+P(3) = 1
and since all are equally probable we have
p=1/3
Now we look at the problem which asks for all such permutation where number 2 appears before any other even number
Since there are 10 even numbers and whatever position they occupy the digit 2 will occur as many number of times before other even numbers as any other even digit Therefore
p =1/10
number of ways to select 10 positions for odd number = C(20 10)
and there are 10! possible arrangements so its 10!*C(20 10)
It leaves place for even numbers which we have to arrange such that we place 2 before any other even number since 2 can be placed in only one way that is before all remaining even numbers
Rest even numbers can be ordered in 9! ways
so number of ways to place 2 before even numbers is = 10! C(20 10) * 9!
Total ways to place 20 digits is 20!
P = 9!/10! =1/10
Probability Problems
Problem An urn contains 5 red, 6 blue,8 green balls. If 3 balls are randomly selected. what is probability of drawing 3 balls of
i)same color
Sample Space: number of ways of drawing 3 balls is C(19 3)
Event Space: number of ways of drawing same color balls = number of ways of drawing 3 red balls + number of ways of drawing 3 green ball + number of ways of drawing 3 blue balls
= C(5 3) + C(6 3) + C(8 3)
without replacement
P =(C(5 3) + C(6 3) + C(8 3)) / C(19 3)
with replacement
P = (5/19)^3 + (8/3)^3 + (8/19)^3
ii)different colors
we want one ball of each color so its
C(5 1)*C(8 1)*C(6 1)
with replacement it would be
(5/19)(6/19)(8/19)
Problem If there are 12 persons in the room, what is probability that no two of them celebrate b'day in same month
Solution
Sample space : since each person can have their b'day in any of the 12 month so its (12)^12
Event space : 12*11*10 ...1 = 12!
P = 12!/12^12
Conditional Probability Problems
Problem Consider 3 urns Urn A contains 2 white and 4 red balls; urn B contains 8 white and 4 red balls and urn C contains 1 white and 3 red balls . If one ball is selected from each urn, what is probability
that ball chosen from urn A was white given that exactly 2 white balls were selected
Solution:
P(A) : probability of selecting white ball from A. similarly P(B) P(C)
P(W2) : probability of selecting exactly two white balls independent of any other event
P(AW2) : white ball from A and exactly one white from B and C = P(A)*P(exactly one white from B and C )
P(A|W2) = P(AW2)/P(W2)
Probability of selecting exactly one white from B and C = P(BC')+P(B'C)
since B and C are independent events
its P(B)P(C') + P(B')P(C)
Probability of selecting exactly two white ball i.e P(W) =
P(ABC')+P(AB'C)+P(A'BC) = P(A)P(B)P(C')+P(A)P(B')P(C)+P(A')P(B)P(C)
since events A B and C are independent so P(ABC) =P(A)P(B)P(C)
P(A|W2) = P(A)* (P(B)P(C') + P(B')P(C)) / P(A)P(B)P(C')+P(A)P(B')P(C)+P(A')P(B)P(C)
Problem In a college 52% are women. 5% students are majoring in CS.2% of students are women majoring in CS.A student is selected at random what is probability
i)that student is female given that student is CS major
Solution
P(F|C) = P(FC) / P(C)
P(F) = .53 P(C) = .05
P(FC) = .02
If it had been "2% of women are majoring in CS" we would have taken P(C|F) instead
P(F|C) = .02/.05
Problem 5% of men and .25% of women are colorblind.A color blind person is chosen at random. what is probability of this person being male.Assume equal number of men and women.
Solution
we need to find P(M|C)
P(M|C) = P(MC)/P(C)
given data is
P(C|M) = .05 P(C|W) =.0025 P(M)=P(W) =.50
P(C) = P(M)P(C|M) + P(W)P(C|W)
P(MC)= P(C/M)P(M)
Observation
When probability is given like t% of A are B
it means P(B|A), when A is the sample space then it becomes P(B)
Like in the problem above when it says
5% of student are women, we are given P(W|S) i.e P(W)
.25% of women are colorblind, we have P(C|W)
Problem Stores A, B and C have 50, 75 and 100 employees, and, respectively, 50, 60 and 70% of these are women. Resignations are equally likely among all employees, regardless of sex.One employee resigns and this is woman. what is probability that she works in store C
Solution we need to find P(C|W)
P(C|W) = P(CW)/P(W)
given data is
P(W|A) = .50 P(W|B) = .60 P(W|C) =.70
n(A) = 50 n(B)=75 n(C)=100
P(W) = P(AW) + P(BW) + P(CW)
= P(W|A)P(A) + P(W|B)P(B)+P(W|C)P(C)
P(A) = n(A) / (n(A)+n(B)+n(C)) similarly for P(B) and P(C)
P(CW)= P(W|C)P(C)
Problem Two cards are chosen at random without replacement
Events: B both cards are ace, A ace of spades is chosen, C atleast one ace is chosen
Find P(B/A),P(B/C)
P(B/A) = P(AB)/P(A) = |AB| / |A|
|A| is number of outcomes in which ace of spades is chosen out of 2 chosen cards = 1*51
since there are two possibilites for ace of spade, it can be first or second card so 2*51 outcomes
|AB| = choose ace of spades and one other spade from remaining 3 = 1*3
and ace of spade can be first or second card so 2*1*3
P(B/A) = 3/51
ii)P(B/C) = P(BC)/P(C) =|BC|/|C|
here lets take case when order doesnot matters whether its first ace or second
Atleast one ace means total hands of card - none ace card
= (52 2) - (48 2) = 198
or we can find exactly one ace + exactly two ace to get atleas one ace
P(B/C) = (4 2) / 198
Some terminology
Probability Distribution(pd)
pd of a random variable X is description of the probabilities associated with possible values of X
sum(P(X=i)) = 1 ; for all possible values of X
that is sum of probability distribution over all the values of random variable is always 1
problems on Probability density
www.ma.utexas.edu/users/geir/teaching/m362k/dailyhw9solns.pdf
Probability mass function(pmf)
PD can be described by function that specifies probability at each possible value of X
fX(x) = P(X=x)
Variance of X
sum{over all random values} x^2f(x) - (Ex)^2
Var(X) = E[ (X - E(X))2] = E(X2) - E(X)2
Properties of Variance
E(cX) = cE(X)
E(c) =c
E(X+Y)=E(X)+E(Y)
var(c) = 0
var(cx)=c^2 * var(x)
var(x+y) = var(x) + var(y) if x and y are independent
Probability Distributions
Probability of k success in n independent trials
For n independent trial where result is either Failure or Success we have bijection with bitstring, let 1 represent success and 0 failure then in bit string of size n we need to have exactly k 1's which is C(n k)
and probability for n trials will be pkqn-k
binomial distribution b(k,n,p) = C(n k)pkqn-k
Expected Value and Variance of B(n,p)
If X is binomial random variable with probability p and total experiment n then expected value and variance depends on p and n only with following equation
E(X) = np because each trial results in random value 1 and 0 so mean for single trial is
1*p+0*(1-p )= p so for n trial its np
and Variance = np(1-p)
because variance for single trial is (x-u)^2 *f(x) that is (1-p)^2*p+(0-p)^2 * (1-p) =p(1-p)
In Bernoulli trial we have k success but here we run the trial until first success
When we have n-1 failures and 1 success on nth trial we have probability as
(1-p)^n-1*p this is known as geometric distribution
for x = 1,2,3 ..
distribution is
x p(x)
----------
1 p
2 (1-p)p
3 (1-p)^2*p
4 (1-p)^3 * p
.
n (1-p)^n-1 * p
Sum of probabilities
when infinite number of trials
sum(0;-) ( p+(1-p)p+(1-p)^2 * p .................... ) = 1
when k failures and then success
sum(0;k)P(X=r) = ( p+(1-p)p+(1-p)^2 * p ...................(1-p)^k * p) = 1- (1-p)^k+1
Expected Value
E(x) = (i=1 to n)xP(x)
= p + 2(1-p)p + 3 (1-p)^2 p + .......n(1-p)^n-1 p
multiply both side by (1-p)
(1-p)E(x) = (1-p)p + 2(1-p)^2 p + 3 (1-p)^2 p + .......n(1-p)^n p)
subtracting 2 from 1
E(x) - (1-p)E(x) = p + (1-p)p + (1-p)^2 p ............n(1-p)^n p)
consider n to be infinity
pE(x) = p(1+(1-p) + (1-p)^2+ ,...........)
= p(1/p)
E(x) = 1/p
Variance is (1-p)/(p)^2
Negative Binomial distribution
until r success from n trials
E(x) = r/p and Variance = r(1-p)/p^2
f(x) = C(x-1,r-1)(1-p)^x-r * p^r
Hypergeometric Distribution
Problems on Random Variable and Expected Value
Problem Two balls are chosen from the urn containing 8 white 4 black and 2 orange balls.Suppose that we win 2 points for each black ball and lose 1 point for each white ball. X denotes our winnings what are possible values of x and probability associated with each
Lets say for selection (W,B) and (B,W) we get the wining X as +1
P(X = 1) = P(W,B)+P(B,W) = 2* 8/14*4/13 =. 3516
similarly for others we can find
Problem Consider value of random variable as
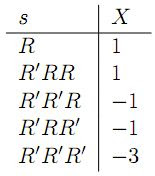i)Find P(X>0) where P(R) = 18/38 and P(R') = 28/38
Solution P(X>0) = P(X=1) which is
P(R) + P(R'RR) assuming independent event we can write P(R'RR) = P(R')P(R)P(R)
ii)Find E(X)
E(x) = (1,n) Σ xP(X=x)
we construct probability distribution
x P(x)
---------------------------
+1 P(R)+P(R'RR)
-1 P(R'R'R)+P(R'RR')
-3 P(R'R'R')
Problem Consider 4 bus carrying 40, 33, 25, 50 students resp.One of the student is selected at random Let X denote number of students in the bus carrying this randomly selected student. One of the bus driver is also randomly selected. Let Y denote number of students on this bus
Find E(X) and E(Y)
so
x p(x)
----------------------
40 40/148
33 33/148
25 25/148
50 50/148
E(x) = 39.28
Value of Y is also same as X but probability of selection of driver from a particular bus is 1/4 since there are only 4 drivers one for each bus
x p(y)
--------------------
40 1/4
33 1/4
25 1/4
50 1/4
Variance(X)
Problem Suppose we toss fair coin until head comes up. X represent number of tosses what is E(x)distribution
x p
1 1/2 (H)
2 1/2*1/2 (TH)
3 1/2*1/2*1/2 (TTH) ......
E(x) = (0 to .. ) i(1/2^i)
= 1/(1/2) = 2
Problem Each sample of water has .10 chance of containing pollutant Find probability that in next 18 sample atleast 4 contain pollutant
P(X >= 4) = sum(x=4;18) (18 x) p^x q^18-x
or P(X>=4) = 1 - P( X < 4)
Poisson Distribution
Example
Let t be expected number of occurrence of event year
divide in to n equal intervals and assume that in any given interval the number of occurence of event is either 1 or 0 The probability of occurrence of event is then t/n
subjected to above assumption binomial distribution gives the probability of there being r occurence of event in n intervals
The assumption is important because if two occurrences of event can happen in single interval then trinomial distribution would be required.To ensure this assumption is valid n must be sufficiently large such that the intervals are sufficiently small
P(X=r) = C(n r) (t/n)^r (1-t/n)^n-r
by solving it we get (t^r/r!) e^-t
Sum of probabilities
(1+t/1! + t/2! + .....)e^-t =e^t * e^-t =1
//normal distribution
Solution
We do not have any discrete time intervals in this problem the event space is on real axes. we can fin d answer to such question using the plot on real axes
Let x axis represent the time line for P1 and y axis be time line for P2
points on line y=x show the time when both of them arrive at the same time
In condition we are given that they wait for interval of time 10minutes that is if P1 arrives at time t then P2 either should arrive 10min before or 10min after P1. So our region is now bounded
which is total area - 2*area of remaining triangles
that is 60*60 - 2*(1/2* (60-10)*(60-10)) = 3600 - 2500 =1100
probability is 1100/3600 = 11/36
Normal Distribution
symmetric bell shaped curve
represented as N(mean, variance) or X ~ N(m,sd^2) meaning X is normally distributed with mean m and standard deviation sd
about 2/3rd of all cases fall within one standard deviation of mean
P(mean - sd <=X <= mean+sd) = .6826
about 95% fall within 2sd
P(mean - 2sd <=X <= mean+2sd) = .9544
Standard Normal variable
convert into standarized normal variable
z = (x- m)/sd
this changes X in to standarized normalization with m=0 and sd =1
z ~ N(0,1)
Properties
i) p(z<=a) = f(a) when a is positive
= 1-f(-a) when a is negative
because 1-f(a) will be symmetrical to f(-a) for a>0
ii)p(z>=a) = 1-f(a)
iii)p(a<=z<=b) = f(b) -f(a)
iv)p(-a<=z<=a) = 2f(a) -1
Problem Consider X~ N(25000, 10000^2). Find P(x<=10000))
standard variable z = (x-25000)/10000
now for x =10000 we have z = -1.5 so
p(x<=10000) = p(z<=-1.5) =1-f(1.5)
Problem In family with 11 children what is probability that there will be more boys then girls
Mean for binomial distribution is Np = 11*1/2 = 5.5
variance =Npq = 5.5*1/2 = 2.75
for binomial it is P(x>=6)
for normal we would say P(z>=5.5)
Countable set : A set is countable if it is finite or has same cardinality as set of natural numbers.
If E F G are three events then
1) only E occurs
means F and G donot occur so EF'G'
2)both E and G but not F
EGF'
3) none of the event occurs
E'F'G'
4)at least one of the event occurs
(E'F'G')' => E U F U G
5)at least two events occurs
EF U EG U FG U EFG
6)all occurs
EFG
7) at most one of them occurs
exactly one of them occurs or none occurs
EF'G' U E'FG' U E'F'G U E'F'G'
8) at most 2 of them occurs
none occurs U exactly one occurs U exactly two occurs
Observations
1) none event occurs(E'F'G') is not complement of all event occurs (EFG)
 |
| Fig. all event occurs |
 |
| Fig none event occur |
Inclusion and Exclusion
P(AB) : probability of events A and B occuring together (intersection)P(A) probability of event A independent of any other event
P(A U B) = P(A) + P(B) - P(AB)
P(E U F U G) =P(E) + P(F) + P(G) - P(EF) - P(FG) - P(GE) + P(EFG)
P(at least 1 event) = 1- P(neither of 3 events occurs)
Conditional Probability
P(B/A) = P(AB)/P(A)
P(ABC) = P(A/BC)P(BC)
= P(A/BC) P(B/C) P(C)
since we can write
P(AB) = P(B/A) P(A) or
P(AB) = P(A/B) P(B)
Some Counting problems
Problem Find number of ways in which digit 1 appears before digit 4 in permutations of number 12345
Solution
Since for any permutation
number 1 will appear either before 4 or after 4, and number of ways in
which 1 can appear before 4 = number of ways in which 1 appears after 4number of permutations = permutations in which 1 appears before 4 + permutations in which 1 appears after 4 i.e 2(n) = 5!
n=5!/2
Problem In how many of permutations of number 12345 is first digit greater than second digit
Solution1
we will look at each digit 1 2 3 4 5 at position 2 and will find number
of permutations in which first digit is less than second digit
1) second digit is 1
no digit is less than 1 so we have 0 cases
2) second digit is 2
at first place we can have 1 and in remaining 3! i.e 1*3!
similarly
3)second digit 3 first place can be occupied by 1 2
2 * 3!
4) second digit 4
3*4!
5) second digit 5
4*3!
total permutaions in which first digit is less than second = 3!(1+2+3+4) = 10*3!
total permutations in which first digit is greater than second = 5!-10!*3! = 5!/2
1/2(5!)
Solution 2
Since for every permutation abcd (a > b)
there will be also be permutation bacd so all cases are equally likely that 1/2 of these will have first digit greater than second
Problem Suppose we randomly select a permutation from 20! permutations of 1,2,3,4, .....20. what is probability that 2 appears at earlier position than any other even number
Solution 1
for any permutation of number say of digits 1,2,3
123
132
213
231
321
312
Probability of any digit appearing a particular position is equally likely
In above case at position 1, one, two and three all appears twice at position 2 also they appear equal number of time at other positions.
At positon 1 either one can appear or two or three so
P(1)+P(2)+P(3) = 1
and since all are equally probable we have
p=1/3
Now we look at the problem which asks for all such permutation where number 2 appears before any other even number
Since there are 10 even numbers and whatever position they occupy the digit 2 will occur as many number of times before other even numbers as any other even digit Therefore
p =1/10
Solution 2
number will be of form even and odd like EEEEOEOE.. number of ways to select 10 positions for odd number = C(20 10)
and there are 10! possible arrangements so its 10!*C(20 10)
It leaves place for even numbers which we have to arrange such that we place 2 before any other even number since 2 can be placed in only one way that is before all remaining even numbers
Rest even numbers can be ordered in 9! ways
so number of ways to place 2 before even numbers is = 10! C(20 10) * 9!
Total ways to place 20 digits is 20!
P = 9!/10! =1/10
Problem An urn contains 5 red, 6 blue,8 green balls. If 3 balls are randomly selected. what is probability of drawing 3 balls of
i)same color
Sample Space: number of ways of drawing 3 balls is C(19 3)
Event Space: number of ways of drawing same color balls = number of ways of drawing 3 red balls + number of ways of drawing 3 green ball + number of ways of drawing 3 blue balls
= C(5 3) + C(6 3) + C(8 3)
without replacement
P =(C(5 3) + C(6 3) + C(8 3)) / C(19 3)
with replacement
P = (5/19)^3 + (8/3)^3 + (8/19)^3
ii)different colors
we want one ball of each color so its
C(5 1)*C(8 1)*C(6 1)
with replacement it would be
(5/19)(6/19)(8/19)
Problem If there are 12 persons in the room, what is probability that no two of them celebrate b'day in same month
Solution
Sample space : since each person can have their b'day in any of the 12 month so its (12)^12
Event space : 12*11*10 ...1 = 12!
P = 12!/12^12
Conditional Probability Problems
Problem Consider 3 urns Urn A contains 2 white and 4 red balls; urn B contains 8 white and 4 red balls and urn C contains 1 white and 3 red balls . If one ball is selected from each urn, what is probability
that ball chosen from urn A was white given that exactly 2 white balls were selected
Solution:
P(A) : probability of selecting white ball from A. similarly P(B) P(C)
P(W2) : probability of selecting exactly two white balls independent of any other event
P(AW2) : white ball from A and exactly one white from B and C = P(A)*P(exactly one white from B and C )
P(A|W2) = P(AW2)/P(W2)
Probability of selecting exactly one white from B and C = P(BC')+P(B'C)
since B and C are independent events
its P(B)P(C') + P(B')P(C)
Probability of selecting exactly two white ball i.e P(W) =
P(ABC')+P(AB'C)+P(A'BC) = P(A)P(B)P(C')+P(A)P(B')P(C)+P(A')P(B)P(C)
since events A B and C are independent so P(ABC) =P(A)P(B)P(C)
P(A|W2) = P(A)* (P(B)P(C') + P(B')P(C)) / P(A)P(B)P(C')+P(A)P(B')P(C)+P(A')P(B)P(C)
Problem In a college 52% are women. 5% students are majoring in CS.2% of students are women majoring in CS.A student is selected at random what is probability
i)that student is female given that student is CS major
Solution
P(F|C) = P(FC) / P(C)
P(F) = .53 P(C) = .05
P(FC) = .02
If it had been "2% of women are majoring in CS" we would have taken P(C|F) instead
P(F|C) = .02/.05
Problem 5% of men and .25% of women are colorblind.A color blind person is chosen at random. what is probability of this person being male.Assume equal number of men and women.
Solution
we need to find P(M|C)
P(M|C) = P(MC)/P(C)
given data is
P(C|M) = .05 P(C|W) =.0025 P(M)=P(W) =.50
P(MC)= P(C/M)P(M)
Observation
When probability is given like t% of A are B
it means P(B|A), when A is the sample space then it becomes P(B)
Like in the problem above when it says
5% of student are women, we are given P(W|S) i.e P(W)
.25% of women are colorblind, we have P(C|W)
Problem Stores A, B and C have 50, 75 and 100 employees, and, respectively, 50, 60 and 70% of these are women. Resignations are equally likely among all employees, regardless of sex.One employee resigns and this is woman. what is probability that she works in store C
Solution we need to find P(C|W)
P(C|W) = P(CW)/P(W)
given data is
P(W|A) = .50 P(W|B) = .60 P(W|C) =.70
n(A) = 50 n(B)=75 n(C)=100
P(W) = P(AW) + P(BW) + P(CW)
= P(W|A)P(A) + P(W|B)P(B)+P(W|C)P(C)
P(A) = n(A) / (n(A)+n(B)+n(C)) similarly for P(B) and P(C)
P(CW)= P(W|C)P(C)
Problem Two cards are chosen at random without replacement
Events: B both cards are ace, A ace of spades is chosen, C atleast one ace is chosen
Find P(B/A),P(B/C)
Solution
P(B/A) probability that both cards are ace when given that ace of spade is chosenP(B/A) = P(AB)/P(A) = |AB| / |A|
|A| is number of outcomes in which ace of spades is chosen out of 2 chosen cards = 1*51
since there are two possibilites for ace of spade, it can be first or second card so 2*51 outcomes
|AB| = choose ace of spades and one other spade from remaining 3 = 1*3
and ace of spade can be first or second card so 2*1*3
P(B/A) = 3/51
ii)P(B/C) = P(BC)/P(C) =|BC|/|C|
here lets take case when order doesnot matters whether its first ace or second
Atleast one ace means total hands of card - none ace card
= (52 2) - (48 2) = 198
or we can find exactly one ace + exactly two ace to get atleas one ace
P(B/C) = (4 2) / 198
Some terminology
Probability Distribution(pd)
pd of a random variable X is description of the probabilities associated with possible values of X
sum(P(X=i)) = 1 ; for all possible values of X
that is sum of probability distribution over all the values of random variable is always 1
problems on Probability density
www.ma.utexas.edu/users/geir/teaching/m362k/dailyhw9solns.pdf
Probability mass function(pmf)
PD can be described by function that specifies probability at each possible value of X
fX(x) = P(X=x)
Variance of X
sum{over all random values} x^2f(x) - (Ex)^2
Var(X) = E[ (X - E(X))2] = E(X2) - E(X)2
Properties of Variance
E(cX) = cE(X)
E(c) =c
E(X+Y)=E(X)+E(Y)
var(c) = 0
var(cx)=c^2 * var(x)
var(x+y) = var(x) + var(y) if x and y are independent
Probability Distributions
Bernoulli Trial and Binomial distribution
Each performance of an experiment with only two independent outcome is bernoulli trial Probability of k success in n independent trials
For n independent trial where result is either Failure or Success we have bijection with bitstring, let 1 represent success and 0 failure then in bit string of size n we need to have exactly k 1's which is C(n k)
and probability for n trials will be pkqn-k
binomial distribution b(k,n,p) = C(n k)pkqn-k
 |
| Fig Bernoulli trial |
Expected Value and Variance of B(n,p)
If X is binomial random variable with probability p and total experiment n then expected value and variance depends on p and n only with following equation
E(X) = np because each trial results in random value 1 and 0 so mean for single trial is
1*p+0*(1-p )= p so for n trial its np
and Variance = np(1-p)
because variance for single trial is (x-u)^2 *f(x) that is (1-p)^2*p+(0-p)^2 * (1-p) =p(1-p)
Geometric Distribution
Instead of fixed number of trials as in bernoulli here trials are conducted until success is obtained In Bernoulli trial we have k success but here we run the trial until first success
When we have n-1 failures and 1 success on nth trial we have probability as
(1-p)^n-1*p this is known as geometric distribution
for x = 1,2,3 ..
distribution is
x p(x)
----------
1 p
2 (1-p)p
3 (1-p)^2*p
4 (1-p)^3 * p
.
n (1-p)^n-1 * p
Sum of probabilities
when infinite number of trials
sum(0;-) ( p+(1-p)p+(1-p)^2 * p .................... ) = 1
when k failures and then success
sum(0;k)P(X=r) = ( p+(1-p)p+(1-p)^2 * p ...................(1-p)^k * p) = 1- (1-p)^k+1
Expected Value
E(x) = (i=1 to n)xP(x)
= p + 2(1-p)p + 3 (1-p)^2 p + .......n(1-p)^n-1 p
multiply both side by (1-p)
(1-p)E(x) = (1-p)p + 2(1-p)^2 p + 3 (1-p)^2 p + .......n(1-p)^n p)
subtracting 2 from 1
E(x) - (1-p)E(x) = p + (1-p)p + (1-p)^2 p ............n(1-p)^n p)
consider n to be infinity
pE(x) = p(1+(1-p) + (1-p)^2+ ,...........)
= p(1/p)
E(x) = 1/p
Variance is (1-p)/(p)^2
Negative Binomial distribution
until r success from n trials
E(x) = r/p and Variance = r(1-p)/p^2
f(x) = C(x-1,r-1)(1-p)^x-r * p^r
Hypergeometric Distribution
Problems on Random Variable and Expected Value
Problem Two balls are chosen from the urn containing 8 white 4 black and 2 orange balls.Suppose that we win 2 points for each black ball and lose 1 point for each white ball. X denotes our winnings what are possible values of x and probability associated with each
Solution
Find sample space for 2 selected balls then find X that is winning for that selectionLets say for selection (W,B) and (B,W) we get the wining X as +1
P(X = 1) = P(W,B)+P(B,W) = 2* 8/14*4/13 =. 3516
similarly for others we can find
Problem Consider value of random variable as
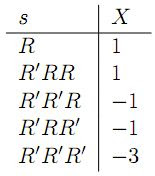
Solution P(X>0) = P(X=1) which is
P(R) + P(R'RR) assuming independent event we can write P(R'RR) = P(R')P(R)P(R)
ii)Find E(X)
E(x) = (1,n) Σ xP(X=x)
we construct probability distribution
x P(x)
---------------------------
+1 P(R)+P(R'RR)
-1 P(R'R'R)+P(R'RR')
-3 P(R'R'R')
Problem Consider 4 bus carrying 40, 33, 25, 50 students resp.One of the student is selected at random Let X denote number of students in the bus carrying this randomly selected student. One of the bus driver is also randomly selected. Let Y denote number of students on this bus
Find E(X) and E(Y)
Solution
value of X is number of students in the bus since students can be selected from any of the busso
x p(x)
----------------------
40 40/148
33 33/148
25 25/148
50 50/148
E(x) = 39.28
Value of Y is also same as X but probability of selection of driver from a particular bus is 1/4 since there are only 4 drivers one for each bus
x p(y)
--------------------
40 1/4
33 1/4
25 1/4
50 1/4
Variance(X)
Problem Suppose we toss fair coin until head comes up. X represent number of tosses what is E(x)distribution
x p
1 1/2 (H)
2 1/2*1/2 (TH)
3 1/2*1/2*1/2 (TTH) ......
E(x) = (0 to .. ) i(1/2^i)
= 1/(1/2) = 2
Problem Each sample of water has .10 chance of containing pollutant Find probability that in next 18 sample atleast 4 contain pollutant
Solution
X number of sample that contains pollutant its bernoulli trial with p=.10 and q =.9 n =18P(X >= 4) = sum(x=4;18) (18 x) p^x q^18-x
or P(X>=4) = 1 - P( X < 4)
Poisson Distribution
Example
Let t be expected number of occurrence of event year
divide in to n equal intervals and assume that in any given interval the number of occurence of event is either 1 or 0 The probability of occurrence of event is then t/n
subjected to above assumption binomial distribution gives the probability of there being r occurence of event in n intervals
The assumption is important because if two occurrences of event can happen in single interval then trinomial distribution would be required.To ensure this assumption is valid n must be sufficiently large such that the intervals are sufficiently small
P(X=r) = C(n r) (t/n)^r (1-t/n)^n-r
by solving it we get (t^r/r!) e^-t
Sum of probabilities
(1+t/1! + t/2! + .....)e^-t =e^t * e^-t =1
//normal distribution
Geometric Probability
Problem
Two friends agree to meet at a park with the following conditions. Each
will reach the park between 4 pm and 5 pm and will see if the other
has already arrived. if not, they will wait for 10 minutes or the end
of the hour whichever is earlier are leave. what is the probability
that the two will not meet? Solution
We do not have any discrete time intervals in this problem the event space is on real axes. we can fin d answer to such question using the plot on real axes
Let x axis represent the time line for P1 and y axis be time line for P2
points on line y=x show the time when both of them arrive at the same time
In condition we are given that they wait for interval of time 10minutes that is if P1 arrives at time t then P2 either should arrive 10min before or 10min after P1. So our region is now bounded
which is total area - 2*area of remaining triangles
that is 60*60 - 2*(1/2* (60-10)*(60-10)) = 3600 - 2500 =1100
probability is 1100/3600 = 11/36
Normal Distribution
symmetric bell shaped curve
represented as N(mean, variance) or X ~ N(m,sd^2) meaning X is normally distributed with mean m and standard deviation sd
about 2/3rd of all cases fall within one standard deviation of mean
P(mean - sd <=X <= mean+sd) = .6826
about 95% fall within 2sd
P(mean - 2sd <=X <= mean+2sd) = .9544
Standard Normal variable
convert into standarized normal variable
z = (x- m)/sd
this changes X in to standarized normalization with m=0 and sd =1
z ~ N(0,1)
Properties
i) p(z<=a) = f(a) when a is positive
= 1-f(-a) when a is negative
because 1-f(a) will be symmetrical to f(-a) for a>0
ii)p(z>=a) = 1-f(a)
iii)p(a<=z<=b) = f(b) -f(a)
iv)p(-a<=z<=a) = 2f(a) -1
Problem Consider X~ N(25000, 10000^2). Find P(x<=10000))
standard variable z = (x-25000)/10000
now for x =10000 we have z = -1.5 so
p(x<=10000) = p(z<=-1.5) =1-f(1.5)
Problem In family with 11 children what is probability that there will be more boys then girls
Mean for binomial distribution is Np = 11*1/2 = 5.5
variance =Npq = 5.5*1/2 = 2.75
for binomial it is P(x>=6)
for normal we would say P(z>=5.5)
No comments:
Post a Comment