Definition and example of a NFA with epsilon transitions.
Remember, epsilon is the zero length string, so it can be any where
in the input string, front, back, between any symbols.
There is a conversion algorithm from a NFA with epsilon transitions to
a NFA without epsilon transitions.
Consider the NFA-epsilon move machine M = { Q, sigma, delta, q0, F}
Q = { q0, q1, q2 }
sigma = { a, b, c } and epsilon moves
q0 = q0
F = { q2 }
sigma plus epsilon
delta | a | b | c |epsilon
------+------+------+------+-------
q0 | {q0} | phi | phi | {q1}
------+------+------+------+-------
q1 | phi | {q1} | phi | {q2}
------+------+------+------+-------
q2 | phi | phi | {q2} | {q2}
------+------+------+------+-------
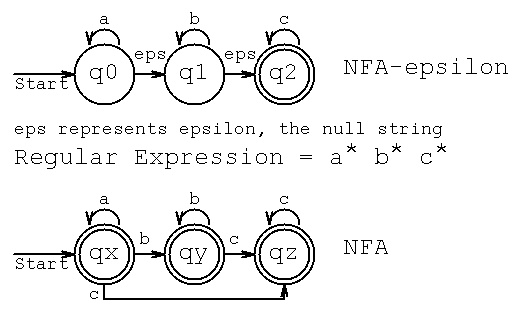
The language accepted by the above NFA with epsilon moves is
the set of strings over {a,b,c} including the null string and
all strings with any number of a's followed by any number of b's
followed by any number of c's. ("any number" includes zero)
Now convert the NFA with epsilon moves to a NFA
M = ( Q', sigma, delta', q0', F')
First determine the states of the new machine, Q' = the epsilon closure
of the states in the NFA with epsilon moves. There will be the same
number of states but the names can be constructed by writing the state
name as the set of states in the epsilon closure. The epsilon closure
is the initial state and all states that can be reached directly
by one or more epsilon moves.
Thus q0 in the NFA-epsilon becomes {q0,q1,q2} because the machine can
move from q0 to q1 by an epsilon move, then check q1 and find that
it can move from q1 to q2 by an epsilon move.
q1 in the NFA-epsilon becomes {q1,q2} because the machine can move from
q1 to q2 by an epsilon move.
q2 in the NFA-epsilon becomes {q2} just to keep the notation the same. q2
can go nowhere except q2, that is what phi means, on an epsilon move.
We do not show the epsilon transition of a state to itself here, but,
beware, we will take into account the state to itself epsilon transition
when converting NFA's to regular expressions.
The initial state of our new machine is {q0,q1,q2} the epsilon closure
of q0
The final state(s) of our new machine is the new state(s) that contain
a state symbol that was a final state in the original machine.
The new machine accepts the same language as the old machine,
thus same sigma.
So far we have for out new NFA
Q' = { {q0,q1,q2}, {q1,q2}, {q2} } or renamed { qx, qy, qz }
sigma = { a, b, c }
F' = { {q0,q1,q2}, {q1,q2}, {q2} } or renamed { qx, qy, qz }
q0 = {q0,q1,q2} or renamed qx
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | | |
------------+--------------+--------------+--------------
qy or {q1,q2} | | |
------------+--------------+--------------+--------------
qz or {q2} | | |
------------+--------------+--------------+--------------
Now we fill in the transitions. Remember that a NFA has transition
entries that are sets. Further, the names in the transition entry
sets must be only the state names from Q'.
Very carefully consider each old machine transitions in the first row.
You can ignore any "phi" entries and ignore the "epsilon" column.
In the old machine delta(q0,a)=q0 thus in the new machine
delta'({q0,q1,q2},a)={q0,q1,q2} this is just because the new machine
accepts the same language as the old machine and must at least have the
the same transitions for the new state names.
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | |
------------+--------------+--------------+--------------
qy or {q1,q2} | | |
------------+--------------+--------------+--------------
qz or {q2} | | |
------------+--------------+--------------+--------------
No more entries go under input a in the first row because
old delta(q1,a)=phi, delta(q2,a)=phi
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | |
------------+--------------+--------------+--------------
qy or {q1,q2} | phi | |
------------+--------------+--------------+--------------
qz or {q2} | phi | |
------------+--------------+--------------+--------------
Now consider the input b in the first row, delta(q0,b)=phi,
delta(q1,b)={q2} and delta(q2,b)=phi. The reason we considered
q0, q1 and q2 in the old machine was because out new state
has symbols q0, q1 and q2 in the new state name from the
epsilon closure. Since q1 is in {q0,q1,q2} and
delta(q1,b)=q1 then delta'({q0,q1,q2},b)={q1,q2}. WHY {q1,q2} ?,
because {q1,q2} is the new machines name for the old machines
name q1. Just compare the zeroth column of delta to delta'. So we have
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | {{q1,q2}} |
------------+--------------+--------------+--------------
qy or {q1,q2} | phi | |
------------+--------------+--------------+--------------
qz or {q2} | phi | |
------------+--------------+--------------+--------------
Now, because our new qx state has a symbol q2 in its name and
delta(q2,c)=q2 is in the old machine, the new name for the old q2,
which is qz or {q2} is put into the input c transition in row 1.
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | {{q1,q2}} | {{q2}} or qz
------------+--------------+--------------+--------------
qy or {q1,q2} | phi | |
------------+--------------+--------------+--------------
qz or {q2} | phi | |
------------+--------------+--------------+--------------
Now, tediously, move on to row two ..., column b ...
You are considering all transitions in the old machine, delta,
for all old machine state symbols in the name of the new machines states.
Fine the old machine state that results from an input and translate
the old machine state to the corresponding new machine state name and
put the new machine state name in the set in delta'. Below are the
"long new state names" and the renamed state names in delta'.
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | {{q1,q2}} | {{q2}} or {qz}
------------+--------------+--------------+--------------
qy or {q1,q2} | phi | {{q1,q2}} | {{q2}} or {qz}
------------+--------------+--------------+--------------
qz or {q2} | phi | phi | {{q2}} or {qz}
------------+--------------+--------------+--------------
inputs
delta' | a | b | c <-- input alphabet sigma
---+------+------+-----
/ qx | {qx} | {qy} | {qz}
/ ---+------+------+-----
Q' qy | phi | {qy} | {qz}
\ ---+------+------+-----
\ qz | phi | phi | {qz}
---+------+------+-----
The figure above labeled NFA shows this state transition table.
It seems rather trivial to add the column for epsilon transitions,
but we will make good use of this in converting regular expressions
to machines. regular-expression -> NFA-epsilon -> NFA -> DFA.

No comments:
Post a Comment