An important question is: How efficient is an algorithm or piece of code? Efficiency covers lots of resources, including:
Be careful to differentiate between:
The time required by a method is proportional to the number of "basic operations" that it performs. Here are some examples of basic operations:
Other methods may perform different numbers of operations, depending on the value of a parameter or a field. For example, for the array implementation of the List class, the remove method has to move over all of the items that were to the right of the item that was removed (to fill in the gap). The number of moves depends both on the position of the removed item and the number of items in the list. We call the important factors (the parameters and/or fields whose values affect the number of operations performed) the problem size or the input size.
When we consider the complexity of a method, we don't really care about the exact number of operations that are performed; instead, we care about how the number of operations relates to the problem size. If the problem size doubles, does the number of operations stay the same? double? increase in some other way? For constant-time methods like the size method, doubling the problem size does not affect the number of operations (which stays the same).
Furthermore, we are usually interested in the worst case: what is the most operations that might be performed for a given problem size (other cases -- best case and average case -- are discussed below). For example, as discussed above, the remove method has to move all of the items that come after the removed item one place to the left in the array. In the worst case, all of the items in the array must be moved. Therefore, in the worst case, the time for remove is proportional to the number of items in the list, and we say that the worst-case time for remove is linear in the number of items in the list. For a linear-time method, if the problem size doubles, the number of operations also doubles.
TEST YOURSELF #1
Assume that lists are implemented using an array. For each of the following List methods, say whether (in the worst case) the number of operations is independent of the size of the list (is a constant-time method), or is proportional to the size of the list (is a linear-time method):
Constant and linear times are not the only possibilities. For example, consider method createList:
Recall that we don't care about the exact time, just how the time depends on the problem size. For method createList, the "problem size" is the value of N (because the number of operations will be different for different values of N). It is clear that the time for the N calls (and therefore the time for method createList) is not independent of N (so createList is not a constant-time method). Is it proportional to N (linear in N)? That would mean that doubling N would double the number of operations performed by createList. Here's a table showing the value of 0+1+2+...+(N-1) for some different values of N:
Clearly, the value of the sum does more than double when the value of N doubles, so createList is not linear in N. In the following graph, the bars represent the lengths of the list (0, 1, 2, ..., N-1) for each of the N calls.
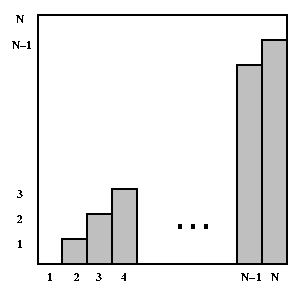
The value of the sum (0+1+2+...+(N-1)) is the sum of the areas of the individual bars. You can see that the bars fill about half of the square. The whole square is an N-by-N square, so its area is N2; therefore, the sum of the areas of the bars is about N2/2. In other words, the time for method createList is proportional to the square of the problem size; if the problem size doubles, the number of operations will quadruple. We say that the worst-case time for createList is quadratic in the problem size.
TEST YOURSELF #2
Consider the following three algorithms for determining whether anyone in the room has the same birthday as you.
Algorithm 1: You say your birthday, and ask whether anyone in the room has the same birthday. If anyone does have the same birthday, they answer yes.
Algorithm 2: You tell the first person your birthday, and ask if they have the same birthday; if they say no, you tell the second person your birthday and ask whether they have the same birthday; etc, for each person in the room.
Algorithm 3: You only ask questions of person 1, who only asks questions of person 2, who only asks questions of person 3, etc. You tell person 1 your birthday, and ask if they have the same birthday; if they say no, you ask them to find out about person 2. Person 1 asks person 2 and tells you the answer. If it is no, you ask person 1 to find out about person 3. Person 1 asks person 2 to find out about person 3, etc.
Question 1: For each algorithm, what is the factor that can affect the number of questions asked (the "problem size")?
Question 2: In the worst case, how many questions will be asked for each of the three algorithms?
Question 3: For each algorithm, say whether it is constant, linear, or quadratic in the problem size in the worst case.
Answer:
Question 1: The problem size is the number of people in the room.
Question 2: Assume there are N people in the room. In algorithm 1 you always ask 1 question. In algorithm 2, the worst case is if no one has your birthday. Here you have to ask every person to figure this out. This is N questions. In algorithm 3, the worst case is the same as algorithm 2. The number of questions is 1 + 2 + 3 + ... + N-1 + N. We showed before that this sum is N(N+1)/2.
Question 3: Given the number of questions you can see that algorithm 1 is constant time, algorithm 2 is linear time, and algorithm 3 is quadratic time in the problem size.
Formal definition:
For example, consider T(N) = 3 * N2 + 5. We can show that T(N) is O(N2) by choosing c = 4 and n0 = 2. This is because for all values of N greater than 2:
3 * N2 + 5 <= 4 * N2
T(N) is not O(N), because whatever constant c and value n0 you choose, I can always find a value of N greater than n0 so that 3 * N2 + 5 is greater than c * N.
In general, we may want to consider the best and average time requirements of a method as well as its worst-case time requirements. Which is considered the most important will depend on several factors. For example, if a method is part of a time-critical system like one that controls an airplane, the worst-case times are probably the most important (if the plane is flying towards a mountain and the controlling program can't make the next course correction until it has performed a computation, then the best-case and average-case times for that computation are not relevant -- the computation needs to be guaranteed to be fast enough to finish before the plane hits the mountain).
On the other hand, if occasionally waiting a long time for an answer is merely inconvenient (as opposed to life-threatening), it may be better to use an algorithm with a slow worst-case time and a fast average-case time, rather than one with so-so times in both the average and worst cases.
Note that calculating the average-case time for a method can be tricky. You need to consider all possible values for the important factors, and whether they will be distributed evenly.
However, it is important to note that constants do not matter in terms of the question of how an algorithm "scales" (i.e., how does the algorithm's time change when the problem size doubles). Although an algorithm that requires N2 time will always be faster than an algorithm that requires 10*N2 time, for both algorithms, if the problem size doubles, the actual time will quadruple.
When two algorithms have different big-O time complexity, the constants and low-order terms only matter when the problem size is small. For example, even if there are large constants involved, a linear-time algorithm will always eventually be faster than a quadratic-time algorithm. This is illustrated in the following table, which shows the value of 100*N (a time that is linear in N) and the value of N2/100 (a time that is quadratic in N) for some values of N. For values of N less than 104, the quadratic time is smaller than the linear time. However, for all values of N greater than 104, the linear time is smaller.
- CPU (time) usage
- memory usage
- disk usage
- network usage
Be careful to differentiate between:
- Performance: how much time/memory/disk/... is actually used when a program is run. This depends on the machine, compiler, etc. as well as the code.
- Complexity: how do the resource requirements of a program or algorithm scale, i.e., what happens as the size of the problem being solved gets larger.
The time required by a method is proportional to the number of "basic operations" that it performs. Here are some examples of basic operations:
- one arithmetic operation (e.g., +, *).
- one assignment
- one test (e.g., x == 0)
- one read
- one write (of a primitive type)
Other methods may perform different numbers of operations, depending on the value of a parameter or a field. For example, for the array implementation of the List class, the remove method has to move over all of the items that were to the right of the item that was removed (to fill in the gap). The number of moves depends both on the position of the removed item and the number of items in the list. We call the important factors (the parameters and/or fields whose values affect the number of operations performed) the problem size or the input size.
When we consider the complexity of a method, we don't really care about the exact number of operations that are performed; instead, we care about how the number of operations relates to the problem size. If the problem size doubles, does the number of operations stay the same? double? increase in some other way? For constant-time methods like the size method, doubling the problem size does not affect the number of operations (which stays the same).
Furthermore, we are usually interested in the worst case: what is the most operations that might be performed for a given problem size (other cases -- best case and average case -- are discussed below). For example, as discussed above, the remove method has to move all of the items that come after the removed item one place to the left in the array. In the worst case, all of the items in the array must be moved. Therefore, in the worst case, the time for remove is proportional to the number of items in the list, and we say that the worst-case time for remove is linear in the number of items in the list. For a linear-time method, if the problem size doubles, the number of operations also doubles.
- the constructor
- add (to the end of the list)
- add (at a given position in the list)
- isEmpty
- contains
- get
- constructor: This method allocates the initial array, sets current to -1 and sets numItems to 0. This has nothing to do with the sequence size and is constant-time.
- add (to the end of the list): In the worst case, the array was full and you have to allocate a new, larger array, and copy all items. In this case the number of operations is proportional to the size of the list. If the array is not full, this is a constant-time operation (because all you have to do is copy one value into the array and increment numItems).
- add (at a given position in the list): As for the other version of add, if the array is full, time proportional to the size of the list is required to copy the values from the old array to the new array. However, even if the array is not full, this version of add can require time proportional to the size of the list. This is because, when adding at position k, all of the items in positions k to the end must be moved over. In the worst case (when the new item is added at the beginning of the list), this requires moving all items over, and that takes time proportional to the number of items in the list.
- isEmpty: This method simply returns the result of comparing numItems with 0; this is a constant=time operation.
- contains: This method involves looking at each item in the list in turn to see if it is equal to the given item. In the worst case (the given item is at the end of the list or is not in the list at all), this takes time proportional to the size of the list.
- get: This method checks for a bad position and either throws an exception or returns the value in the given position in the array. In either case it is independent of the size of the list and so it is a constant-time operation.
Constant and linear times are not the only possibilities. For example, consider method createList:
List createList( int N ) {
List L = new List();
for (int k=1; k<=N; k++) L.add(0, new Integer(k));
return L;
}
Note that, for a given N, the for-loop above is equivalent to:L.add(0, new Integer(1) );
L.add(0, new Integer(2) );
L.add(0, new Integer(3) );
...
L.add(0, new Integer(N) );
If we assume that the initial array is large enough to hold N items, then the number of operations for each call to add is proportional to the number of items in the list when add is called (because it has to move every item already in the array one place to the right to make room for the new item at position 0). For the N calls shown above, the list lengths are: 0, 1, 2, ..., N-1. So what is the total time for all N calls? It is proportional to 0 + 1 + 2 + ... + N-1.Recall that we don't care about the exact time, just how the time depends on the problem size. For method createList, the "problem size" is the value of N (because the number of operations will be different for different values of N). It is clear that the time for the N calls (and therefore the time for method createList) is not independent of N (so createList is not a constant-time method). Is it proportional to N (linear in N)? That would mean that doubling N would double the number of operations performed by createList. Here's a table showing the value of 0+1+2+...+(N-1) for some different values of N:
| N | 0+1+2+...+(N-1) |
| 4 | 6 |
| 8 | 28 |
| 16 | 120 |

Algorithm 1: You say your birthday, and ask whether anyone in the room has the same birthday. If anyone does have the same birthday, they answer yes.
Algorithm 2: You tell the first person your birthday, and ask if they have the same birthday; if they say no, you tell the second person your birthday and ask whether they have the same birthday; etc, for each person in the room.
Algorithm 3: You only ask questions of person 1, who only asks questions of person 2, who only asks questions of person 3, etc. You tell person 1 your birthday, and ask if they have the same birthday; if they say no, you ask them to find out about person 2. Person 1 asks person 2 and tells you the answer. If it is no, you ask person 1 to find out about person 3. Person 1 asks person 2 to find out about person 3, etc.
Question 1: For each algorithm, what is the factor that can affect the number of questions asked (the "problem size")?
Question 2: In the worst case, how many questions will be asked for each of the three algorithms?
Question 3: For each algorithm, say whether it is constant, linear, or quadratic in the problem size in the worst case.
Answer:
Question 1: The problem size is the number of people in the room.
Question 2: Assume there are N people in the room. In algorithm 1 you always ask 1 question. In algorithm 2, the worst case is if no one has your birthday. Here you have to ask every person to figure this out. This is N questions. In algorithm 3, the worst case is the same as algorithm 2. The number of questions is 1 + 2 + 3 + ... + N-1 + N. We showed before that this sum is N(N+1)/2.
Question 3: Given the number of questions you can see that algorithm 1 is constant time, algorithm 2 is linear time, and algorithm 3 is quadratic time in the problem size.
Big-O Notation
We express complexity using big-O notation. For a problem of size N:- a constant-time method is "order 1": O(1)
- a linear-time method is "order N": O(N)
- a quadratic-time method is "order N squared": O(N2)
Formal definition:
- A function T(N) is O(F(N)) if for some constant c and for all values of N greater than some value n0:
For example, consider T(N) = 3 * N2 + 5. We can show that T(N) is O(N2) by choosing c = 4 and n0 = 2. This is because for all values of N greater than 2:
How to Determine Complexities
In general, how can you determine the running time of a piece of code? The answer is that it depends on what kinds of statements are used.- Sequence of statements
statement 1; statement 2; ... statement k;
(Note: this is code that really is exactly k statements; this is not an unrolled loop like the N calls to add shown above.) The total time is found by adding the times for all statements:total time = time(statement 1) + time(statement 2) + ... + time(statement k)
If each statement is "simple" (only involves basic operations) then the time for each statement is constant and the total time is also constant: O(1). In the following examples, assume the statements are simple unless noted otherwise. - if-then-else statements
if (condition) { sequence of statements 1 } else { sequence of statements 2 }Here, either sequence 1 will execute, or sequence 2 will execute. Therefore, the worst-case time is the slowest of the two possibilities: max(time(sequence 1), time(sequence 2)). For example, if sequence 1 is O(N) and sequence 2 is O(1) the worst-case time for the whole if-then-else statement would be O(N). - for loops
for (i = 0; i < N; i++) { sequence of statements }The loop executes N times, so the sequence of statements also executes N times. Since we assume the statements are O(1), the total time for the for loop is N * O(1), which is O(N) overall. - Nested loopsFirst we'll consider loops where the number of iterations of the inner loop is independent of the value of the outer loop's index. For example:
for (i = 0; i < N; i++) { for (j = 0; j < M; j++) { sequence of statements } }The outer loop executes N times. Every time the outer loop executes, the inner loop executes M times. As a result, the statements in the inner loop execute a total of N * M times. Thus, the complexity is O(N * M). In a common special case where the stopping condition of the inner loop is j < N instead of j < M (i.e., the inner loop also executes N times), the total complexity for the two loops is O(N2).Now let's consider nested loops where the number of iterations of the inner loop depends on the value of the outer loop's index. For example:
for (i = 0; i < N; i++) { for (j = i+1; j < N; j++) { sequence of statements } }Now we can't just multiply the number of iterations of the outer loop times the number of iterations of the inner loop, because the inner loop has a different number of iterations each time. So let's think about how many iterations that inner loop has. That information is given in the following table:
Value of i Number of iterations of inner loop 0 N 1 N-1 2 N-2 ... ... N-2 2 N-1 1
TEST YOURSELF #3 What is the worst-case complexity of the each of the following code fragments?
- Two loops in a row:
for (i = 0; i < N; i++) { sequence of statements } for (j = 0; j < M; j++) { sequence of statements }How would the complexity change if the second loop went to N instead of M? - A nested loop followed by a non-nested loop:
for (i = 0; i < N; i++) { for (j = 0; j < N; j++) { sequence of statements } } for (k = 0; k < N; k++) { sequence of statements } - A nested loop in which the number of times the inner loop executes depends on the value of the outer loop index:
for (i = 0; i < N; i++) { for (j = N; j > i; j--) { sequence of statements } }
- The first loop is O(N) and the second loop is O(M). Since you don't know which is bigger, you say this is O(N+M). This can also be written as O(max(N,M)). In the case where the second loop goes to N instead of M the complexity is O(N). You can see this from either expression above. O(N+M) becomes O(2N) and when you drop the constant it is O(N). O(max(N,M)) becomes O(max(N,N)) which is O(N).
- The first set of nested loops is O(N2) and the second loop is O(N). This is O(max(N2,N)) which is O(N2).
- This is very similar to our earlier example of a nested loop where the number of iterations of the inner loop depends on the value of the index of the outer loop. The only difference is that in this example the inner-loop index is counting down from N to i+1. It is still the case that the inner loop executes N times, then N-1, then N-2, etc, so the total number of times the innermost "sequence of statements" execites is O(N2).
- Two loops in a row:
- Statements with method calls:When a statement involves a method call, the complexity of the statement includes the complexity of the method call. Assume that you know that method f takes constant time, and that method g takes time proportional to (linear in) the value of its parameter k. Then the statements below have the time complexities indicated.
f(k); // O(1) g(k); // O(k)
When a loop is involved, the same rule applies. For example:for (j = 0; j < N; j++) g(N);
has complexity (N2). The loop executes N times and each method callg(N)is complexity O(N).
TEST YOURSELF #4 For each of the following loops with a method call, determine the overall complexity. As above, assume that method f takes constant time, and that method g takes time linear in the value of its parameter.
1. for (j = 0; j < N; j++) f(j); 2. for (j = 0; j < N; j++) g(j); 3. for (j = 0; j < N; j++) g(k);
Answer:
- Each call to f(j) is O(1). The loop executes N times so it is N x O(1) or O(N).
- The first time the loop executes j is 0 and g(0) takes "no operations". The next time j is 1 and g(1) takes 1 operations. The last time the loop executes j is N-1 and g(N-1) takes N-1 operations. The total work is the sum of the first N-1 numbers and is O(N2).
- Each time through the loop g(k) takes k operations and the loop executes N times. Since you don't know the relative size of k and N, the overall complexity is O(N x k).
Best-case and Average-case Complexity
Some methods may require different amounts of time on different calls, even when the problem size is the same for both calls. For example, consider the add method that adds an item to the end of the list. In the worst case (the array is full), that method requires time proportional to the number of items in the list (because it has to copy all of them into the new, larger array). However, when the array is not full, add will only have to copy one value into the array, so in that case its time is independent of the length of the list; i.e., constant time.In general, we may want to consider the best and average time requirements of a method as well as its worst-case time requirements. Which is considered the most important will depend on several factors. For example, if a method is part of a time-critical system like one that controls an airplane, the worst-case times are probably the most important (if the plane is flying towards a mountain and the controlling program can't make the next course correction until it has performed a computation, then the best-case and average-case times for that computation are not relevant -- the computation needs to be guaranteed to be fast enough to finish before the plane hits the mountain).
On the other hand, if occasionally waiting a long time for an answer is merely inconvenient (as opposed to life-threatening), it may be better to use an algorithm with a slow worst-case time and a fast average-case time, rather than one with so-so times in both the average and worst cases.
Note that calculating the average-case time for a method can be tricky. You need to consider all possible values for the important factors, and whether they will be distributed evenly.
When do Constants Matter?
Recall that when we use big-O notation, we drop constants and low-order terms. This is because when the problem size gets sufficiently large, those terms don't matter. However, this means that two algorithms can have thesame big-O time complexity, even though one is always faster than the other. For example, suppose algorithm 1 requires N2 time, and algorithm 2 requires 10 * N2 + N time. For both algorithms, the time is O(N2), but algorithm 1 will always be faster than algorithm 2. In this case, the constants and low-order terms do matter in terms of which algorithm is actually faster.However, it is important to note that constants do not matter in terms of the question of how an algorithm "scales" (i.e., how does the algorithm's time change when the problem size doubles). Although an algorithm that requires N2 time will always be faster than an algorithm that requires 10*N2 time, for both algorithms, if the problem size doubles, the actual time will quadruple.
When two algorithms have different big-O time complexity, the constants and low-order terms only matter when the problem size is small. For example, even if there are large constants involved, a linear-time algorithm will always eventually be faster than a quadratic-time algorithm. This is illustrated in the following table, which shows the value of 100*N (a time that is linear in N) and the value of N2/100 (a time that is quadratic in N) for some values of N. For values of N less than 104, the quadratic time is smaller than the linear time. However, for all values of N greater than 104, the linear time is smaller.
| N | 100*N | N2/100 |
| 102 | 104 | 102 |
| 103 | 105 | 104 |
| 104 | 106 | 106 |
| 105 | 107 | 108 |
| 106 | 108 | 1010 |
| 107 | 109 | 1012 |