Correctness of Algorithms

What does it mean to produce a correct solution to a problem? We can usually specify precisely what a correct solution would entail. For example, if your GPS produces a correct solution to finding the best route to travel, it might be the route, out of all possible routes from where you are to your desired destination, that will get you there soonest or perhaps the route that has the shortest possible distance or the route that will get you there soonest but also avoids tolls. Of course, the information that your GPS uses to determine a route might not match reality. Unless your GPS can access real-time traffic information, it might assume that the time to traverse a road equals the road's distance divided by the road's speed limit. If the road is congested, however, the GPS might give you bad advice if you're looking for the fastest route. We can still say that the routing algorithm that the GPS runs is correct, however, even if the input to the algorithm is not; for the input given to the routing algorithm, the algorithm produces the fastest route. Now, for some problems, it might be difficult or even impossible to say whether an algorithm produces a correct solution.

Sometimes, however, we can accept that a computer algorithm might produce an incorrect answer, as long as we can control how often it does so. Encryption provides a good example. The commonly used RSA cryptosystem relies on determining whether large numbers-really large, as in hundreds of digits long-are prime. If you have ever written a computer program, you could probably write one that determines whether a number n is prime. It would test all candidate divisors from 2 through n - 1, and if any of these candidates is indeed a divisor of n, then n is composite. If no number between 2 and n - 1 is a divisor of n, then n is prime. But if n is hundreds of digits long, that's a lot of candidate divisors, more than even a really fast computer could check in any reasonable amount of time. Of course, you could make some optimizations, such as eliminating all even candidates once you find that 2 is not a divisor, or stopping once you get to sqrt(n) (since if d is greater than sqrt(n) and d is a divisor of n, then n/ d is less than sqrt(n) and is also a divisor of n; therefore, if n has a divisor, you will find it by the time you get to sqrt(n)). If n is hundreds of digits long, then although sqrt(n) has only about half as many digits as n does, it's still a really large number. The good news is that we know of an algorithm that tests quickly whether a number is prime. The bad news is that it can make errors. In particular, if it declares that n is composite, then n is definitely composite, but if it declares that n is prime, then there's a chance that n is actually composite. But the bad news is not all that bad: we can control the error rate to be really low, such as one error in every 2⁵⁰ times. That's rare enough-one error in about every million billion times-for most of us to be comfortable with using this method to determine whether a number is prime for RSA.

Correctness is a tricky issue with another class of algorithms, called approximation algorithms. Approximation algorithms apply to optimization problems, in which we want to find the best solution according to some quantitative measure. Finding the fastest route, as a GPS does, is one example, where the quantitative measure is travel time. For some problems, we have no algorithm that finds an optimal solution in any reasonable amount of time, but we know of an approximation algorithm that, in a reasonable amount of time, can find a solution that is almost optimal. By "almost optimal;' we typically mean that the quantitative measure of the solution found by the approximation algorithm is within some known factor of the optimal solution's quantitative measure. As long as we specify what the desired factor is, we can say that a correct solution from an approximation algorithm is any solution that is within that factor of the optimal solution.

Some Programs to work with

COUNTING BITS IN AN UNSIGNED INTEGER

Computing the number of 1-bits in an unsigned integer:

/* Counting the Bit Set for an Unsigned Integer */
/*
(A) Loop through all the bits
    Computing time is proportional to the number of bits
(B) Computing time is proportional to the number of bits set
*/

#include <iostream>

using namespace std;


/* bit count for unsigned integer */
/* checking if the first bit == 1 while shifting right
   (25) 
   11001 -> 1100 -> 110 -> 11 -> 1
*/

int bit_countA(unsigned int n){
 int count = 0;
 while(n) {
  count += n & 0x1u;
  n >>= 1;  
 }
 return count;
}


/* sets the right most bit set 1 to 0 */
/* Computing time is proportional to the number of bits set */

int bit_countB(unsigned int n) {
 int count = 0;
 while(n) {
  count ++;
  n &= n - 1;  
 }
 return count;
}

int main()
{
 /* 25 (11001) */
 unsigned int num = 25;

 cout << num <<": # of bits set (A) is " << bit_countA(num) << endl;
 cout << num <<": # of bits set (B) is " << bit_countB(num) << endl;

 return 0;
}

INT STRLEN(CONST CHAR *)

strlen() counts just the visible characters and not the null character.

int strlen1(const char *s) {
    int n=0;
    while (*s++) n++;
    return(n);
}

int strlen2(const char *s) {
    int n=0;
    while (s[n]) n++;
    return(n);
}

CHAR* STRCPY(CHAR *, CONST CHAR*)

char* strcpy1(char s1[], const char s2[]) {
 for(int i=0; i <=strlen(s2); i++) {
  s1[i] = s2[i];
 }
 return s1;
}

char* strcpy2(char *s1, const char *s2) {
 char *p = s1;
 while(*s2!='\0') {
  *s1 = *s2;
  s1++;
  s2++;
 }
        *s1 = '\0';
 return p;
}

char* strcpy3(char *s1, const char *s2) {
 char *p = s1;
 while(*s2) *s1++ = *s2++;
        *s1 = '\0';
 return p;
}

char* strcpy4(char *s1, const char *s2) {
 char *p = s1;
 while(*s1++ = *s2++);
 return p;
}


char* strcpy5(char *s1, const char *s2) {
 int i = 0, j = 0;
 while(s1[i++] = s2[j++]);
 return s1;
}

CHAR * STRDUP ( CHAR *S)

strdup() does dynamic memory allocation for the character array including the end character '\0' and returns the address of the heap memory:

char *strdup (const char *s) {
    char *p = malloc (strlen (s) + 1);   // allocate memory
    if (p != NULL)
        strcpy (p,s);                    // copy string
    return p;                            // return the memory
}

So, what it does is giving us another string identical to the string given by its argument, without requiring us to allocate memory. But we still need to free it, later.

Though strdup() has been widely used, it's not a standard C/C++ library. So, there is an ambiguity regarding which memory allocation function was used and which deallocation function should be used to deallocate the memory: free() or delete()?
So, if the portability of our code is an issue, we should avoid using it.

VOID * MEMCPY ( VOID * DESTINATION, CONST VOID * SOURCE, SIZE_T SZ );

Copy block of memory
Copies the values of sz bytes from the location pointed by source directly to the memory block pointed by destination.
The underlying types of the objects pointed by both the source and destination pointers are irrelevant for this function;
The result is a binary (bit pattern) copy of the data.
The function does not check for any terminating null character in source - it always copies exactly sz bytes.
The behavior of memcpy() is undefined if source and destination overlap.

#include <iostream>
using namespace std;

void *memcpy( void *destination, const void *source, size_t sz ) {
  char *dest = (char *)destination;
  char const *src = (char *)source;

  while (sz--)
    *dest++ = *src++;
  return destination;
}

int main()
{
 char src1[] = "Ludwig Van Beethoven";
 char *src2 = "Franz Liszt ";
 char dest[40];

 cout << "src 1: " << src1 << endl;
 memcpy(dest,src1, strlen(src1)+1);
 cout << "dest: " << dest<< endl;

 cout << "src 2: " << src2 << endl;
 memcpy(dest,src2, strlen(src2)+1);
 cout << "dest: " << dest<< endl;

 return 0;
}

Output is:

src 1: Ludwig Van Beethoven
dest: Ludwig Van Beethoven
src 2: Franz Liszt
dest: Franz Liszt

VOID *MEMMOVE(VOID *DEST, CONST VOID *SRC, SIZE_T SZ)

Memmove() copies n bytes between two memory areas; unlike memcpy(), the areas may overlap. Actually, it is a variant ofmemcpy() that allows the source and destination block to overlap; otherwise it is equivalent (but slightly slower).

#include <iostream>
using namespace std;

void *memcpy(void *dest, const void *src, size_t sz)
{
 char *tmp = (char *)dest;
 char *s = (char *)src;

 while(sz--) {
  *tmp++ = *s++;
 }
 return dest;
}

void *memmove(void *dest, const void *src, size_t sz)
{
 char *tmp, *s;

 if (dest <= src) {
  tmp = (char *) dest;
  s = (char *) src;
  while (sz--)
   *tmp++ = *s++;
 }
 else {
  tmp = (char *) dest + sz;
  s = (char *) src + sz;
  while (sz--)
   *--tmp = *--s;
 }

 return dest;
}

int main()
{
 char src[50] = "Einstein was a very nice person!";

 cout << src << endl;
 memmove(src + 20, src + 15, 17);
 cout << src << endl;

 return 0;
}

Output is:

Einstein was a very nice person!
Einstein was a very very nice person!

VOID * MEMSET ( VOID * DESTINATION, INT SOURCE, SIZE_T SZ );

Sets the first sz bytes of the block of memory pointed by destination to the specified source (interpreted as an unsigned char).

#include <stdio.h>
#include <string.h>

void *MyMemset(void* destination, int source, size_t sz)
{
 char *pt = (char *)destination;
 while(sz--) {
      *pt++ = (unsigned char)(source);
 }
 return destination;
}
 
int main()
{
 char str1[]  = "What the heck is memset?";
 char str2[]  = "What the heck is memset?";
 memset(str1 + 5, '*',8);
 puts(str1);
 MyMemset(str2 + 5, 'x',8);
 puts(str2);
 return 0;
}

Output is:

What ******** is memset?
What xxxxxxxx is memset?

INT MEMCMP (CONST VOID *S1, CONST VOID *S2, SIZE_T SZ )

Compare two blocks of memory.
Compares the first sz bytes of the block of memory pointed by s1 to the first sz bytes pointed by s2, returning zero if they all match or a value different from zero representing which is greater if they do not. Unlike strcmp(), the function does not stop comparing after finding a null character.

#include <iostream>
using namespace std;

int memcmp(const void *s1, const void *s2, size_t sz)
{
 if (sz!= 0) {
  const char *p1 = (const char *)s1;
  const char *p2 = (const char *)s2;
  do {
   if (*p1++ != *p2++)
    return (*--p1 - *--p2);
  } while (--sz!= 0);
 }
 return (0);
}

int main ()
{
  char s1[] = "abc123";
  char s2[] = "abc12A";

  int n = memcmp ( s1, s2, sizeof(s1) );

  if (n > 0) 
   cout << s1 << " is greater than " << s2 << endl;
  else if (n < 0) 
   cout << s1 << " is less than " << s2 << endl;
  else 
   cout << s1 << " is the same as " << s2 << endl;

  return 0;
}

Output is:

abc123 is less than abc12A

CONVERTING STRING TO INTEGER (ATOI())

example A

#include <sstream>
int str2intA(const string &str) {
       stringstream ss(str);
       int n;
       ss >> n;
       return n;
}

example B

int str2intB(const string &str){
 int n = 0;
 int len =str.length();
 for(int i = 0; i < len; i++) {
  n *= 10;
  n += str[i]-'0';
 }
 return n;
}

CONVERTING INTEGER TO STRING (ITOA())

example A

#include <sstream>
string int2strA(int n) {
 stringstream ss;
 ss << n; 
 return ss.str();
}

example B

string int2strB(int numb) {
 int i=0;
 int end=10;
 char* temp = new char[end];
 
 //store one digit at a time 
 for(i = 0; numb > 0; i++) {
  temp[i] = (numb % 10) + '0';
  numb /= 10;
 }

 // temp has the number in reverse order
 int len = i;
 int ii = 0;
 string s = new char[len];
 while(i > 0) s[ii++] = temp[--i];
 s.erase(len);
 delete temp;
 return s;
}

example C

#include <iostream>
#include <cstring>

using namespace std;

// reverse the string
void reverse(char *s)
{
 int sz = strlen(s);
 char c;
 int i, j;
 for(i = 0, j = sz -1; i < j; i++, j--) {
  c = s[i];
  s[i] = s[j];
  s[j] = c;
 }
}

// itoa
void int2strC(int n, char *s)
{
 int i = 0;
 while( n ) {
  s[i++] =  n % 10 + '0';
  n /= 10;
 }
 s[i] = '\0';
 cout << "before the reverse s = " << s << endl;
 reverse(s);
}

int main()
{
 char s[10];
 int n = 987654321;
 cout << "input n = " << n << endl;
 int2strC(n, s);
 cout << "output s = " << s << endl;
 return 0;
}

Output from the run:

input n = 987654321
before the reverse s = 123456789
output s = 987654321

ASCII STRING TO FLOAT - ATOF()

#include <iostream>
using namespace std;

double atofA(char s[]) 
{
 double d = 0, power = 1;
 int sign = 1;
 int i = 0;

 if(s[i] == '-' ) sign = -1;
 i++;
 while(s[i]) {
  if(s[i] == '.') break;
  d = d * 10 + (s[i] - '0');
  i++;
 }
 i++;
 power = 0.1;
 while(s[i]) {
  d += (s[i] - '0')*power;
  power /= 10.0;
  i++;
 }

 return d*sign;
}

int main()
{
 double d = atofA("-314.1592");
 cout.precision(7);
 cout  << d << endl;
 return 0;
}

REVERSING AN INTEGER: 345->543

#include <iostream>

using namespace std;

int reverse_int(int n)
{
 int m = 0;
 while(n >= 1) {
  m *= 10;
  m += n % 10;
  n = n / 10;
 }
 return m;
}

int main()
{
 int n;
 cin >> n;
 cout << "reverse of " << n << " is " << reverse_int(n) << endl;
 return 0;
}

Output:

345
reverse of 345 is 543

MULTIPLICATION WITHOUT MULTIPLICATION - RUSSIAN PEASANT MULTIPLICATION

238*13 without any multiplication operation.

Actually, the algorithm we're going to use is known as Russian Peasant Multiplication or
wiki-Ancient Egyptian multiplication.

// Russian Peasant Multiplication 

#include <iostream>
#include <iomanip>
using namespace std;

int RussianPeasant(int a, int b)
{
 int x = a,  y = b;
 int val = 0;
 cout << left << setw(5) << x << left << setw(5) << y << left << setw(5) << val << endl;
 while (x > 0) {
  if (x % 2 == 1) val = val + y;
  y = y << 1;  // double
  x = x >> 1;  // half
  cout << left << setw(5) << x << left << setw(5) << y << left << setw(5) << val << endl; 
 }
 return val;
}

int main() {
 RussianPeasant(238, 13);
 return 0;
}

The output should look like this:

238  13   0
119  26   0
59   52   26
29   104  78
14   208  182
7    416  182
3    832  598
1    1664 1430
0    3328 3094

Actually, the multiplication is known as Russian Peasant Multiplication. Whenever x is odd, the value of y is added to val until xequals to zero, and then it returns 3094.

REVERSING A STRING

Example A

#include <iostream>
#include <cstring>

void reverse_string(char s[]) {
 int i,j,c;
 for(i = 0, j = strlen(s)-1; i < j ; i++, j-- ) {
  c = s[i];
  s[i] = s[j];
  s[j] = c;
 }
}

int main() {
 char s[] ="reverse me";
 reverse_string(s);
 std::cout << s << std::endl;
 return 0;
}

Example B Printing a String Reversed 
Here we have two print functions, one for normal and the other one for printing a string in reverse.

#include <iostream>

using namespace std;

void normalPrint(char *s)
{
 if(*s) {
  putchar(*s);
  normalPrint(s+1);
 }
}
void reversePrint(char *s)
{
 if(*s) {
  reversePrint(s+1);
  putchar(*s);
 }
}

int main() 
{
 char *str = "Normal or Reverse";
 normalPrint(str);
 cout << endl;
 reversePrint(str);
 cout << endl;
 return 0;
}

Output is:

Normal or Reverse
esreveR ro lamroN

FINDING THE FIRST UN-REPEATING (NON-REPEATING) CHARACTER - METHOD A

This code is using map. 

1. Put all characters into a map.
2. If necessary (repeated), it will increment a counter which is the 2nd component of map, value.
3. Then, traverse the string and search the map. If found and counter value is 1, return that character.
4. Complexity: traversing (O(N)), searching balanced binary tree (O(log(N)) => O(N + log(N)) => O(N)

// Returning a character which is the first non-repeated in a string
#include <iostream>
#include <string>
#include <map>

using namespace std;
char find(string s)
{
 map<char,int> myMap;
 int len = s.length();
 for(int i = 0; i < len; i++) ++myMap[s[i]];
 for(int i = 0; i < len; i++) 
  if(myMap.find(s[i])->second == 1) return s[i];

 return 0;
}

int main()
{
 string s="abudabi";
 cout << find(s);
 return 0;
}

FINDING THE FIRST UN-REPEATING (NON-REPEATING) CHARACTER - METHOD B

This method is using simple array utilizing the inversion of character and integer.

Complexity: O(N) - It needs just two traversing.

// Returning a character which is the first non-repeated in a string
#include <iostream>
using namespace std;

char find(char* s)
{
 int myArr[256] = {0};
 int len = strlen(s);
 for(int i = 0; i < len; i++) 
  myArr[s[i]]++;

 for(int i = 0; i < len; i++)
  if(myArr[s[i]] == 1) return s[i];

 return 0;
}

int main()
{
 char* s="abudabi";
 cout << find(s);  // output 'u'
 return 0;
}

BINARY SEARCH A

#include <iostream>

using namespace std;

int bsearch(int [], int, int, int);

int main()
{
 const int arrSize = 100;
 int arr[arrSize];

 for (int i = 0; i <= arrSize -1; i++) {
  arr[i] = i;
 }

 int x = 35;
 int low = 0;
 int high = arrSize -1;
 int found = bsearch(arr, x, low, high);
 if(found == -1) {
  cout << "Could not find " << x << endl;
  return 0;
 }
 cout << "The value " << x << " is at " << found << endl;
 return 0;
}

int bsearch(int arr[], int x, int low, int high) {
 int mid;
 if(high < low) return -1;  // no match 
 while (low <= high) {
  mid = low + (high - low) / 2;
  if(x < arr[mid])
   high = mid - 1;
  else if (x > arr[mid])
   low = mid + 1;
  else
   return mid; // this is match 
 }
}

BINARY SEARCH B - RECURSIVE

int bsearch(int arr[], int x, int low, int high) {
 int mid;
 if(high < low) return -1;  // no match 
 mid = low + (high - low) / 2;
 if(x < arr[mid]) 
  bsearch(arr, x, low, mid - 1);
 else if (x > arr[mid]) 
  bsearch(arr, x, mid + 1, high);
 else
  return mid; // this is match 
}

BIG ENDIAN OR LITTLE ENDIAN (BYTE ORDER)?

If we want to represent a two-byte hex number, say c23g, we'll store it in two sequential bytes c2 followed by 3g. It seems that it's the right way of doing it. This number, stored with the big end first, is called big-endian. Unfortunately, however, a few computers, namely anything with an Intel or Intel-compatible processor, store the bytes reversed, so c23g would be stored in memory as the sequential bytes 3g followed by c2. This storage method is called little-endian.

Endian is important to know when reading or writing data structures, especially across networks so that different application can communicate with each other. Sometimes the endianness is hidden from the developer. Java uses a fixed endianness to store data regardless of the underlying platform's endianness, so data exchanges between two Java applications won't normally be affected by endianness. But other languages, C in particular don't specify an endianness for data storage, leaving the implementation free to choose the endianness that works best for the platform.

On big-endian (PowerPC, SPARC, and Internet), the 32-bit value x01234567 is stored as four bytes 0x01, 0x23, 0x45, 0x67, while on little-endian (Intel x86), it will be stored in reverse order:

 




 

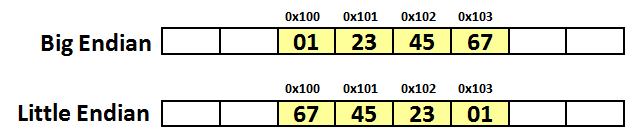
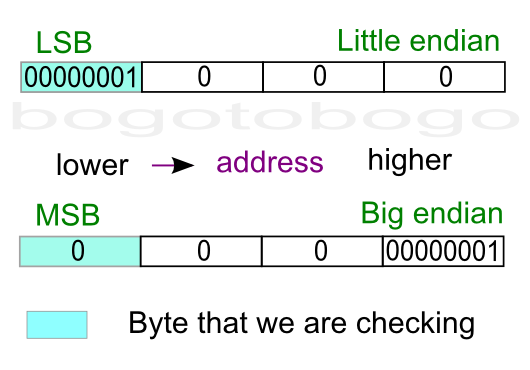
The picture below is a diagram for the example to check if a machine is little endian or big endian. The box shaded blue is the the byte we are checking because it's where a one-byte type (char) will be stored. The diagram shows where an integer (4-byte) value 1is stored.

We can distinguish between the LSB and the MSB because the value 1 as an integer, has the value of 1 for LSN, and the value of 0 for MSB.

Note that a little endian machine will place the 1 (0001x, LSB) into the lowest memory address location. However, a big endian machine will put 0 (0001x, MSB) into the lowest memory address location.

 

Source A

#include <iostream>
using namespace std;

/* if the dereferenced pointer is 1, the machine is little-endian 
   otherwise the machine is big-endian */

int endian() {
 int one = 1;
 char *ptr;
 ptr = (char *)&one;
 return (*ptr);
}

int main()
{
 if(endian()) 
  cout << "little endian\n";
 else
  cout << "big endian\n";
}

Source B

#include <iostream>
using namespace std;

int endian() {
 union {
  int one;
  char ch;
 } endn;

 endn.one = 1;
 return endn.ch;
}

int main()
{
 if(endian()) 
  cout << "little endian\n";
 else
  cout << "big endian\n";
}

It is tempting to use bit operation for this problem. However, bit shift operator works on integer, not knowing the internal byte order, and that property prevents us from using the bit operators to determine byte order.

To check out the endian, we can just print out an integer (4 byte) to a 4-character output with the address of each character.

#include <stdio.h>

int main()
{
 int a = 12345; // x00003039
 char *ptr = (char*)(&a);
 for(int i = 0; i < sizeof(a); i++) {
  printf("%p\t0x%.2x\n", ptr+i, *(ptr+i));
 }
 return 0;
}

Output:

0088F8D8        0x39
0088F8D9        0x30 
0088F8DA        0x00
0088F8DB        0x00

As we see from the output, LSB (0x39) was written first at the lower address, which indicate my machine is little endian.

REMOVING COMMAS

Given a char array {1,234,34,54} Modify the char array so that there is no comma in the most efficient way. We must get a char array {12343454}

#include <iostream>
using namespace std;

void remove_comma(char arr[])
{
 char *b = arr, *c = arr;
 while(*b)
 {
  if(*b == ',') b++;
  else
   *c++ = *b++;
 }
 *c = '\0';
 return;

}

int main()
{
 char arr[] = "1,234,34,54";
 cout << arr << endl;

 remove_comma(arr);

 cout << arr << endl;

    return 0;
}

Output:

1,234,34,54
12343454

HASH TABLE BASED ON K & R

#include <iostream>
using namespace std;

#include 
using namespace std;

#define HASHSIZE 101

struct nlist {       /* table entry: */
       struct nlist *next;   /* next entry in chain */
       char *name;           /* defined name */
       char *defn;           /* replacement text */
};

static struct nlist *hashtab[HASHSIZE];

unsigned hash_function(char *s) {
       unsigned hashval;

       for (hashval = 0; *s != '\0'; s++)
           hashval = *s + 31 * hashval;
       return hashval % HASHSIZE;
}

struct nlist *lookup(char *s) {
       struct nlist *np;

       for (np = hashtab[hash_function(s)];  np != NULL; np = np->next)
           if (strcmp(s, np->name) == 0)
               return np;     /* found */
       return NULL;           /* not found */
}

/* install:  put (name, defn) in hashtab */
struct nlist *install(char *name, char *defn) {
       struct nlist *np;
       unsigned hashval;

       if ((np = lookup(name)) == NULL) { /* not found */
     np = new nlist;
           if (np == NULL || (np->name = _strdup(name)) == NULL)
               return NULL;
           hashval = hash_function(name);
           np->next = hashtab[hashval];
           hashtab[hashval] = np;
       } else       /* already there */
           /*free previous defn */
     delete np->defn;
       if ((np->defn = _strdup(defn)) == NULL)
           return NULL;
       return np;
}

/* uninstall:  take (name, defn) out of hashtab */
int undef(char * name) {
 struct nlist * np1;
 /* name not found */
 if ((np1 = lookup(name)) == NULL)  
  return 1;

 /* name found */
 if((np1 = hashtab[hash_function(name)]) != NULL ) {
  hashtab[hash_function(name)] = np1->next;
  delete np1;
  return 0;
 }
 /* name not found */
 return 1;  
}

void print() {

 struct nlist *np;
 for(int i = 0; i < HASHSIZE; i++) {
  np = hashtab[i];
  if(np) 
   cout << np->name << "-->" << np->defn << " ";
 }
 cout << endl;
}

int main()
{
 install("A","65");
 install("B","66");
 install("C","67");
 install("D","68");
 install("E","69");
 print();
 undef("C");
 print();
 undef("B");
 print();
 return 0;
}

Output from the run:

A-->65 B-->66 C-->67 D-->68 E-->69
A-->65 B-->66 D-->68 E-->69
A-->65 D-->68 E-->69

CALCULATOR BASED ON K & R

/* Calculator based on K & R
  (1) Not working for '(' such as 1+(5-3) 
  (2) Added 
  getop(s);
  push(a2f(s));
 after '+', '-', '*', and '/' to push next number
*/

#include <iostream>
#include <cstring>
#include <cctype>

using namespace std;

int getop(char []);
void push(double);
double pop(void);
int getch(void);
void ungetch(int);
int a2f(char *);
void calc();

int main() 
{
 calc();
 return 0;
}

const int MAXOP = 100;
const char NUMBER = '0';

void calc() {
 int type;
 double op2;
 char s[MAXOP];
  
 while((type = getop(s)) != EOF) {
  switch (type) {
   case NUMBER:
    push(a2f(s));
    break;
   case '+':
    getop(s);
    push(a2f(s));
    push(pop() + pop());
    break;
   case '*':
    getop(s);
    push(a2f(s));
    push(pop() * pop());
    break;
   case '-':
    getop(s);
    push(a2f(s));
    op2 = pop();
    push(pop()-op2);
    break;
   case '/':
    getop(s);
    push(a2f(s));
    op2 = pop();
    if(op2 != 0.0) 
     push(pop() / op2);
    else
     cout << "error: division by zero" << endl;
    break;
   case '\n':
    cout << pop() << endl;
    break;
   default:
    cout << "error: unknown command " << s << endl;
  }
 }
}

// getop(): get next operator or numeric operand 
int getop(char s[]) {
 int i, c;

 while ( (s[0] = c = getch()) == ' ' || c == '\t') 
  ;
 s[1] = '\0';
 if( !isdigit(c) && c != '.')
  return c; // not a number
 i = 0;
 if (isdigit(c)) // collect integer part
  while (isdigit(s[++i] = c = getch()))
   ;
 if (c == '.') // collect fraction
  while (isdigit(s[++i] = c = getch()))
   ;
 s[i] = '\0';
 if (c != EOF )
  ungetch(c);

 return NUMBER;
}

const int BUFSIZE = 100;
char buf[BUFSIZE];
int bufp = 0;

int getch(void) {
 return (bufp > 0) ? buf[--bufp] : cin.get();
}

void ungetch(int c) {
 if (bufp >= BUFSIZE)
  cout << "ungetch(): too many characters\n";
 else
  buf[bufp++] = c;
}

int a2f(char *s) {
 int n = 0;
 while(*s) {
  n *= 10;
  n += (*s++)-'0';
 }
 return n;
}

const int MAXVAL = 100;
int sp = 0;
double val[MAXVAL];

void push(double f) {
 if( sp < MAXVAL )
  val[sp++] = f;
 else
  cout << "error: stack full, can't push "<< f << endl;
}

double pop(void) {
 if (sp > 0)
  return val[--sp];
 else {
  cout << "error: stack empty \n";
  return 0.0;
 }
}

SIZE OF STRUCT

How do we find the number of structures for the given array of structures in the sample code below?

#include <iostream>

using namespace std; 

struct vehicle
{
 int price;
 char type[10];
} car[] = {
 {1,"a"},{2,"b"},{3,"c"}
};

int main() 
{
 cout << "sizeof(car)=" << sizeof(car) << endl;
 cout << "sizeof(*car)=" << sizeof(*car) << endl;
 cout << "sizeof(car)/sizeof(*car)=" << sizeof(car)/sizeof(*car) << endl;
 return 0;
}

Answer is:

sizeof(car)=48
sizeof(*car)=16
sizeof(car)/sizeof(*car)=3

Note that the size of an array of vehicle struct is not 4+1*10 but 16. This is probably due to padding/allignmment:

4 + 1*4 + 1*4 + (1*2+2) = 16

As an exercise, how about the following example:

struct StructA 
{ 
 char ch1; 
 char ch2; 
 int n; 
}; 

struct StructB 
{ 
 char ch1; 
 int n; 
 char ch2; 
}; 

int sizeA = sizeof(StructA); // sizeA = 1 + 1 + (2-padding) + 4 = 8
int sizeB = sizeof(StructB); // sizeB = 1 + (3-padding) + 4 + 1 + (3-padding) = 12

Remember, it is frequently very difficult to predict the sizes of compound datatypes such as a struct or union due to structurepadding. Another reason for using sizeof is readability.

SIZE OF STRUCT & CLASS

#include <iostream>

class con
{
public: 
 struct node
 {
  int data;
  int rest;
 };

 con(){}
};

int main()
{
 con c;
 std::cout << "size of con class =" << sizeof(c);  // size is 1
 return 0;
}

The class is empty, in other words, no members. But the size of the class is 1. Not sure but it seems to be related to the pointer arithmetic(?). However, if we add the following to the structure, things change:

 struct node
 {
  int data;
  int rest;
 } nd;

The the output becomes 4(data)+4(rest)=8. If we use pointer then:

 struct node
 {
  int data;
  int rest;
 } *nd;

the size becomes 4(nd).

REMOVING LEFT SPACE OF A STRING

#include <iostream>
#include <cassert>

using namespace std; 

char *left_space_trim(char *buf, const char *s) {
 assert(buf != NULL);
 assert( s!= NULL);

 while(isspace(*s))
  s++;
 strcpy(buf,s);
 return buf;
}

int main() 
{
 char *srcStr = strdup("  String with left_side spaces");
 char *dstStr = (char*)malloc(strlen(srcStr)+1);
 cout << srcStr << "=>" << left_space_trim(dstStr,srcStr) << endl;

 return 0;
}

Output is:

  String with left_side spaces=>String with left_side spaces

RECTANGLES OVERLAPPING

It is also called OBB/OBB (Oriented Bounding Box) Intersection problem. Here, a brute force method will be presented first, and the other one (separating axes approach) which seems more elegant will come later time.

 

#include <iostream>

class Point
{
public:
 Point(float a, float b):x(a),y(b){}
 float getX() {return x;}
 float getY() {return y;}
private:
 float x, y;
};

class Rect
{
public:
 Rect(Point a, Point b):ul(a),lr(b){}
 float getHeight() {return ul.getY()-lr.getY();}
 float getWidth() {return lr.getX()-ul.getX();}
 float getXmin() {return ul.getX();}
 float getXmax() {return lr.getX();}
 float getYmin() {return lr.getY();}
 float getYmax() {return ul.getY();}
private:
 Point ul,lr;
};

bool overlapped(Rect &r1, Rect &r2)
{
 float height1 = r1.getHeight();
 float height2 = r2.getHeight();
 float width1 = r1.getWidth();
 float width2 = r2.getWidth();
 // case A: No corners inside 
 if(r1.getWidth() >= r2.getWidth()) {
  if(r2.getXmin() >= r1.getXmin() && r2.getXmax() <= r1.getXmax()
   && r2.getYmin() <= r1.getYmin() && r2.getYmax() >= r1.getYmax() ) 
   return true;
 }
 else {
  if(r1.getXmin() >= r2.getXmin() && r1.getXmax() <= r2.getXmax()
   && r1.getYmin() <= r2.getYmin() && r1.getYmax() >= r2.getYmax() ) 
   return true;
 }

 // case B: r2's corner inside r1 rect? (compare r1 with r2)
 // r2's ul (Xmin, Ymax)
 if(r1.getXmin() <= r2.getXmin() && r1.getXmax() >= r2.getXmin()
   && r1.getYmax() >= r2.getYmax() && r1.getYmin() <= r2.getYmax() ) 
   return true;
 // r2's ur (Xmax, Ymax)
 if(r1.getXmin() <= r2.getXmax() && r1.getXmax() >= r2.getXmax()
   && r1.getYmax() >= r2.getYmax() && r1.getYmin() <= r2.getYmax() ) 
   return true;
 // r2's ll (Xmin, Ymin)
 if(r1.getXmin() <= r2.getXmin() && r1.getXmax() >= r2.getXmin()
   && r1.getYmax() >= r2.getYmin() && r1.getYmin() <= r2.getYmin() ) 
   return true;
 // r2's lr (Xmax, Ymin)
 if(r1.getXmin() <= r2.getXmax() && r1.getXmax() >= r2.getXmax()
   && r1.getYmax() >= r2.getYmin() && r1.getYmin() <= r2.getYmin() ) 
   return true;
 return false;
}

int main()
{
 float x1 = 0.0, y1 = 5.0, x2 = 5.0, y2 = 0.0;
 float x3 = 4.0, y3 = 1.0, x4 = 6.0, y4 = -1.0;

 Point pt1(x1,y1), pt2(x2,y2);
 Point pt3(x3,y3), pt4(x4,y4);

 Rect rta(pt1,pt2);
 Rect rtb(pt3,pt4);

 if(overlapped(rta,rtb)) 
  std::cout << "Overlapped: " << std::endl;
 else
  std::cout << "Not overlapped: " << std::endl;

 return 0;
}

FINDING PAIRS OF INTEGERS WHOSE SUM EQUALS TO A GIVEN SUM

The input an ordered array.

We start to check from both ends, and depending on the sum of the pair, we either increment left index or decrement the right index until they meet.

#include <iostream>
using namespace std;

// input sum
// input array, a
// input size of array, sz
// input & output pairs of integers, pair

int fnd(int sum, int *a, int sz, int *pair)
{
    int i = 0, j = sz-1, index = 0, count = 0;

    while(i < j) {
 if(a[i]+a[j] > sum) 
            j--;
 else if(a[i]+a[j] < sum) 
     i++;
 else {
     pair[index++] = a[i++];
     pair[index++] = a[j--];
     count += 2;
        }
    }
    return count;
}

int main()
{
    int sum =18;
    int a[] = {1, 3, 5, 7, 9, 11, 13, 15, 16};
    int size = sizeof(a)/sizeof(int);
    int *pair = new int[size];

    int count = fnd(sum, a, size, pair);

    for(int i = 0; i < count; i++) cout << pair[i] << " ";

    return 0;
}

Google Interview Questions for Software Engineer

1. Why are manhole covers round?
2. What is the difference between a mutex and a semaphore?
   Which one would you use to protect access to an increment operation?
3. A man pushed his car to a hotel and lost his fortune. What happened?
4. Explain the significance of "dead beef".
5. Write a C program which measures the speed of a context switch on a UNIX/Linux system.
6. Given a function which produces a random integer in the range 1 to 5, write a function which produces a random integer in the range 1 to 7.
7. Describe the algorithm for a depth-first graph traversal.
8. Design a class library for writing card games.
9. You need to check that your friend, Bob, has your correct phone number, but you cannot ask him directly.
   You must write a question on a card which and give it to Eve who will take the card to Bob and return the answer to you.
   What must you write on the card, besides the question, to ensure Bob can encode the message so that Eve cannot read your phone number?
10. How are cookies passed in the HTTP protocol?
11. Design the SQL database tables for a car rental database.
12. Write a regular expression which matches an email address.
13. Write a function f(a, b) which takes two character string arguments and returns a string containing only the characters found in both strings in the order of a.
    Write a version which is order N-squared and one which is order N.
14. You are given a source to an application which is crashing when run.
    After running it 10 times in a debugger, you find it never crashes in the same place.
    The application is single threaded, and uses only the C standard library.
    What programming errors could be causing this crash?
    How would you test each one?
15. Explain how congestion control works in the TCP protocol.
16. In Java, what is the difference between final, finally, and finalize?
17. What is multithreaded programming? What is a deadlock?
18. Given a series A,B,C .......Z, AA, AB,AC,AD....AZ,BA,BB...BZ,CA....(Open excel sheet. The names of column represent the series). Given input as number 'n'. Output the 'n' th string of the series. & also vice versa if given string prints its corrsponding string...e.g given AC then its interger is 29 & given 40774 its string value is ABZ..


19. You have a stream of infinite queries (i.e., real time Google search queries that people are entering).
    Describe how you would go about finding a good estimate of 1000 samples from this never ending set of data and then write code for it.


20. Tree search algorithms.
    Write BFS and DFS code, explain run time and space requirements.
    Modify the code to handle trees with weighted edges and loops with BFS and DFS, make the code print out path to goal state.


21. You are given a list of numbers.
    When you reach the end of the list you will come back to the beginning of the list (a circular list).
    Write the most efficient algorithm to find the minimum # in this list.
    Find any given # in the list.
    The numbers in the list are always increasing but you don't know where the circular list begins, i. e., 38, 40, 55, 89, 6, 13, 20, 23, 36.


22. Describe the data structure that is used to manage memory. (stack)


23. What's the difference between local and global variables?


24. If you have 1 million integers, how would you sort them efficiently?
    (modify a specific sorting algorithm to solve this)


25. In Java, what is the difference between static, final, and const.
    (if you don't know Java they will ask something similar for C or C++).


26. Talk about your class projects or work projects
    (pick something easy)... then describe how you could make them more efficient (in terms of algorithms).


27. Suppose you have an NxN matrix of positive and negative integers.
    Write some code that finds the sub-matrix with the maximum sum of its elements.


28. Write some code to reverse a string.


29. Implement division (without using the divide operator, obviously).


30. Write some code to find all permutations of the letters in a particular string.


31. What method would you use to look up a word in a dictionary?


32. Imagine you have a closet full of shirts.
    It's very hard to find a shirt. So what can you do to organize your shirts for easy retrieval?


33. You have eight balls all of the same size. 7 of them weigh the same, and one of them weighs slightly more. How can you fine the ball that is heavier by using a balance and only two weighings?


34. What is the C-language command for opening a connection with a foreign host over the internet?


35. Design and describe a system/application that will most efficiently produce a report of the top 1 million Google search requests. These are the particulars:
    1) You are given 12 servers to work with. They are all dual-processor machines with 4Gb of RAM, 4x400GB hard drives and networked together.(Basically, nothing more than high-end PC's)
    2) The log data has already been cleaned for you. It consists of 100 Billion log lines, broken down into 12 320 GB files of 40-byte search terms per line.
    3) You can use only custom written applications or available free open-source software.


36. There is an array A[N] of N numbers.
    You have to compose an array Output[N] such that Output[i] will be equal to multiplication of all the elements of A[N] except A[i].
    For example Output[0] will be multiplication of A[1] to A[N-1] and Output[1] will be multiplication of A[0] and from A[2] to A[N-1]. Solve it without division operator and in O(N).


37. There is a linked list of numbers of length N.
    N is very large and you don't know N.
    You have to write a function that will return k random numbers from the list.
    Numbers should be completely random.
    Hint: 1. Use random function rand() (returns a number between 0 and 1) and irand() (return either 0 or 1)
    2. It should be done in O(N).


38. Find or determine non existence of a number in a sorted list of N numbers where the numbers range over M, M>> N and N large enough to span multiple disks.
    Algorithm to beat O(log n) bonus points for constant time algorithm.


39. You are given a game of Tic Tac Toe.
    You have to write a function in which you pass the whole game and name of a player.
    The function will return whether the player has won the game or not.
    First you to decide which data structure you will use for the game.
    You need to tell the algorithm first and then need to write the code.
    Note: Some position may be blank in the game? So your data structure should consider this condition also.


40. You are given an array [a1 To an] and we have to construct another array [b1 To bn] where bi = a1*a2*...*an/ai. you are allowed to use only constant space and the time complexity is O(n). No divisions are allowed.


41. How do you put a Binary Search Tree in an array in an efficient manner.
    Hint :: If the node is stored at the ith position and its children are at 2i and 2i+1(I mean level order wise).
    It's not the most efficient way.


42. How do you find out the fifth maximum element in a Binary Search Tree in efficient manner.
    Note: You should not use any extra space. i.e., sorting Binary Search Tree and storing the results in an array and listing out the fifth element.


43. Given a Data Structure having first n integers and next n chars. A = i1 i2 i3 ... iN c1 c2 c3 ... cN.
    Write an in-place algorithm to rearrange the elements of the array ass A = i1 c1 i2 c2 ... in cn


44. Given two sequences of items, find the items whose absolute number increases or decreases the most when comparing one sequence with the other by reading the sequence only once.


45. Given That One of the strings is very very long , and the other one could be of various sizes.
    Windowing will result in O(N+M) solution but could it be better?
    May be NlogM or even better?


46. How many lines can be drawn in a 2D plane such that they are equidistant from 3 non-collinear points?


47. Let's say you have to construct Google maps from scratch and guide a person standing on Gateway of India (Mumbai) to India Gate(Delhi). How do you do the same?


48. Given that you have one string of length N and M small strings of length L.
    How do you efficiently find the occurrence of each small string in the larger one?


49. Given a binary tree, programmatically you need to prove it is a binary search tree.


50. You are given a small sorted list of numbers, and a very very long sorted list of numbers - so long that it had to be put on a disk in different blocks.
    How would you find those short list numbers in the bigger one?


51. Suppose you have given N companies, and we want to eventually merge them into one big company.
    How many ways are there to merge?


52. Given a file of 4 billion 32-bit integers, how to find one that appears at least twice?


53. Write a program for displaying the ten most frequent words in a file such that your program should be efficient in all complexity measures.


54. Design a stack. We want to push, pop, and also, retrieve the minimum element in constant time.


55. Given a set of coin denominators, find the minimum number of coins to give a certain amount of change.


56. Given an array,
    i) find the longest continuous increasing subsequence.
    ii) find the longest increasing subsequence.


57. Suppose we have N companies, and we want to eventually merge them into one big company.
    How many ways are there to merge?


58. Write a function to find the middle node of a single link list.


59. Given two binary trees, write a compare function to check if they are equal or not. Being equal means that they have the same value and same structure.


60. Implement put/get methods of a fixed size cache with LRU replacement algorithm.


61. You are given with three sorted arrays ( in ascending order), you are required to find a triplet ( one element from each array) such that distance is minimum.


62. Distance is defined like this :
    If a[i], b[j] and c[k] are three elements then distance=max(abs(a[i]-b[j]),abs(a[i]-c[k]),abs(b[j]-c[k]))"
    Please give a solution in O(n) time complexity


63. How does C++ deal with constructors and destructors of a class and its child class?


64. Write a function that flips the bits inside a byte (either in C++ or Java).
    Write an algorithm that take a list of n words, and an integer m, and retrieves the mth most frequent word in that list.


65. What's 2 to the power of 64?


66. Given that you have one string of length N and M small strings of length L.
    How do you efficiently find the occurrence of each small string in the larger one?
67. How do you find out the fifth maximum element in an Binary Search Tree in efficient manner.


68. Suppose we have N companies, and we want to eventually merge them into one big company.
    How many ways are there to merge?


69. There is linked list of millions of node and you do not know the length of it.
    Write a function which will return a random number from the list.


70. You need to check that your friend, Bob, has your correct phone number, but you cannot ask him directly.
    You must write a question on a card which and give it to Eve who will take the card to Bob and return the answer to you.
    What must you write on the card, besides the question, to ensure Bob can encode the message so that Eve cannot read your phone number?


71. How long it would take to sort 1 trillion numbers? Come up with a good estimate.


72. Order the functions in order of their asymptotic performance:
    1) 2^n 2) n^100 3) n! 4) n^n


73. There are some data represented by(x,y,z).
    Now we want to find the Kth least data. We say (x1, y1, z1) > (x2, y2, z2) when value(x1, y1, z1) > value(x2, y2, z2) where value(x,y,z) = (2^x)*(3^y)*(5^z).
    Now we cannot get it by calculating value(x,y,z) or through other indirect calculations as lg(value(x,y,z)).
    How to solve it?


74. How many degrees are there in the angle between the hour and minute hands of a clock when the time is a quarter past three?


75. Given an array whose elements are sorted, return the index of the first occurrence of a specific integer.
    Do this in sub-linear time. I.e. do not just go through each element searching for that element.
76. Given two linked lists, return the intersection of the two lists: i.e. return a list containing only the elements that occur in both of the input lists.
77. What's the difference between a hashtable and a hashmap?
78. If a person dials a sequence of numbers on the telephone, what possible words/strings can be formed from the letters associated with those numbers?
79. How would you reverse the image on an n by n matrix where each pixel is represented by a bit?
80. Create a fast cached storage mechanism that, given a limitation on the amount of cache memory, will ensure that only the least recently used items are discarded when the cache memory is reached when inserting a new item.
    It supports 2 functions: String get(T t) and void put(String k, T t).
81. Create a cost model that allows Google to make purchasing decisions on to compare the cost of purchasing more RAM memory for their servers vs. buying more disk space.
82. Design an algorithm to play a game of Frogger and then code the solution.
    The object of the game is to direct a frog to avoid cars while crossing a busy road.
    You may represent a road lane via an array.
    Generalize the solution for an N-lane road.
83. What sort would you use if you had a large data set on disk and a small amount of ram to work with?
84. What sort would you use if you required tight max time bounds and wanted highly regular performance.
85. How would you store 1 million phone numbers?
86. Design a 2D dungeon crawling game. It must allow for various items in the maze - walls, objects, and computer-controlled characters.
    (The focus was on the class structures, and how to optimize the experience for the user as s/he travels through the dungeon.)
87. What is the size of the C structure below on a 32-bit system? On a 64-bit?

    struct foo {
    char a; 
    char* b; 
    };